Prediction of Google Stock Price using RNN

In this we are going to predict the opening price of the stock given the highest, lowest and closing price for that particular day by using RNN-LSTM.

Ref- https://colah.github.io/posts/2015-08-Understanding-LSTMs/

What is RNN?

• Recurrent Neural Networks are the first of its kind State of the Art algorithms that can memorize/remember previous inputs in memory when a huge set of Sequential data is given to it.
• Recurrent Neural Network is a generalization of feedforward neural network that has an internal memory.
• RNN is recurrent in nature as it performs the same function for every input of data while the output of the current input depends on the past one computation.
• After producing the output, it is copied and sent back into the recurrent network. For making a decision, it considers the current input and the output that it has learned from the previous input.
• In other neural networks, all the inputs are independent of each other. But in RNN, all the inputs are related to each other.

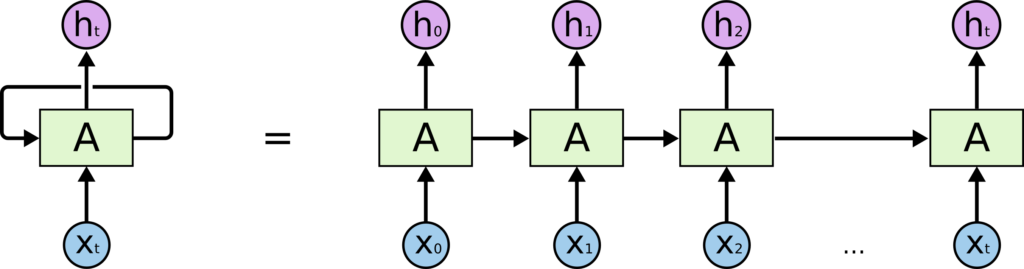
• These loops make recurrent neural networks seem kind of mysterious. However, if you think a bit more, it turns out that they aren’t all that different than a normal neural network.
• A recurrent neural network can be thought of as multiple copies of the same network, each passing a message to a successor.

Different types of RNNs

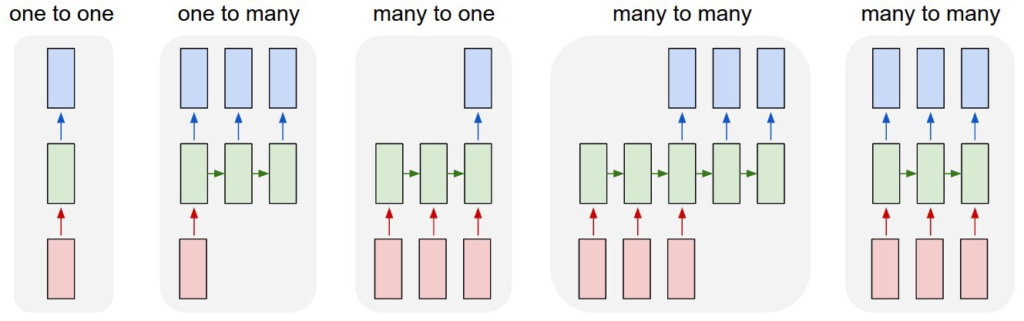
Some examples are-

• One to one It is used for Image Classification. Here input is a single image and output is a single label of the category the image belongs.
• One to many(Sequence output) It is used for Image Captioning. Here the input is an image and output is a group of words which is the caption for the image.
• Many to One(Sequence input) It is used for Sentiment Analysis. Here a given sentence which is a group of words is classified as expressing positive or negative sentiment which is a single output.
• Many to Many(Sequence input and sequence output) It is Machine Translation. A RNN reads a sentence in English and then outputs a sentence in French.
• Synced Many to Many(Synced sequence input and output) It is used for Video Classification where we wish to label each frame of the video.

The Problem of Long-Term Dependencies

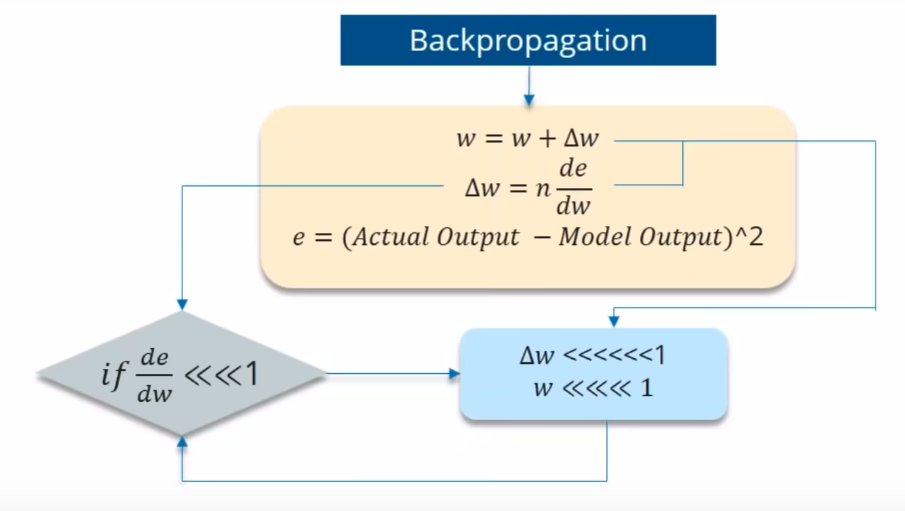
Vanishing Gradient

• Information travels through the neural network from input neurons to the output neurons, while the error is calculated and propagated back through the network to update the weights.
• During the training, the cost function(e) compares your outcomes to your desired output.
• If the partial derivation of error is less than 1, then when it gets multiplied with the learning rate which is also very less won't generate a big change when compared with previous iteration.
• For the vanishing gradient problem, the further you go through the network, the lower your gradient is and the harder it is to train the weights, which has a domino effect on all of the further weights throughout the network.

Exploding Gradient

• We speak of Exploding Gradients when the algorithm assigns a stupidly high importance to the weights, without any reason.
• Exploding gradients are a problem where large error gradients accumulate and result in very large updates to neural network model weights during training.
• This has the effect of your model being unstable and unable to learn from your training data.
• But fortunately, this problem can be easily solved if you truncate or squash the gradients

Long Short Term Memory (LSTM) Networks

• Long Short Term Memory networks – usually just called “LSTMs” – are a special kind of RNN, capable of learning long-term dependencies.
• Generally LSTM is composed of a cell (the memory part of the LSTM unit) and three "regulators", usually called gates, of the flow of information inside the LSTM unit: an input gate, an output gate and a forget gate.
• Intuitively, the cell is responsible for keeping track of the dependencies between the elements in the input sequence.
• The input gate controls the extent to which a new value flows into the cell, the forget gate controls the extent to which a value remains in the cell and the output gate controls the extent to which the value in the cell is used to compute the output activation of the LSTM unit.
• The activation function of the LSTM gates is often the logistic sigmoid function.
• There are connections into and out of the LSTM gates, a few of which are recurrent. The weights of these connections, which need to be learned during training, determine how the gates operate.
• LSTMs are explicitly designed to avoid the long-term dependency problem. Remembering information for long periods of time is practically their default behavior, not something they struggle to learn!

Dataset

You can download the dataset from here

The data used in this notebook is from 19th August,2004 to 7th October,2019. The dataset consists of 7 columns which contain the date, opening price, highest price, lowest price, closing price, adjusted closing price and volume of share for each day.

Steps to build stock prediction model

• Data Preprocessing
• Building the RNN
• Making the prediction and visualization

We will read the data for first 60 days and then predict for the 61st day. Then we will hop ahead bt one day and read the next chunk of data for next sixty days.

The necessary python libraries are imported here-

• numpy is used to perform basic array operations
• pyplot from matplotlib is used to visualize the results
• pandas is used to read the dataset
• MinMaxScaler from sklearn is used scale the data

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.preprocessing import MinMaxScaler

read_csv is used to load the data into the dataframe. We can see the last 5 rows of the dataset using data.tail(). Similarly data.head() can be used to see the first 5 rows of the dataset. date_parser is used for converting a sequence of string columns to an array of datetime instances.

data = pd.read_csv('GOOG.csv', date_parser = True)
data.tail()

	Date	Open	High	Low	Close	Adj Close	Volume
3804	2019-09-30	1220.969971	1226.000000	1212.300049	1219.000000	1219.000000	1404100
3805	2019-10-01	1219.000000	1231.229980	1203.579956	1205.099976	1205.099976	1273500
3806	2019-10-02	1196.979980	1196.979980	1171.290039	1176.630005	1176.630005	1615100
3807	2019-10-03	1180.000000	1189.060059	1162.430054	1187.829956	1187.829956	1621200
3808	2019-10-04	1191.890015	1211.439941	1189.170044	1209.000000	1209.000000	1021092

Here we splitting the data into training and testing dataset. We are going to take data from 2004 to 2018 as training data. Subsequently we are going to take the data of 2019 as testing data.

data_training = data[data['Date']<'2019-01-01'].copy()
data_test = data[data['Date']>='2019-01-01'].copy()

We are dropping the columns Date and Adj Close from the training dataset

data_training = data_training.drop(['Date', 'Adj Close'], axis = 1)

The values in the training data are not in the same range. For getting all the values in between the range 0 to 1 we are going to use MinMaxScalar().This improves the accuracy of prediction.

scaler = MinMaxScaler()
data_training = scaler.fit_transform(data_training)
data_training

array([[3.30294890e-04, 9.44785459e-04, 0.00000000e+00, 1.34908021e-04,
        5.43577404e-01],
       [7.42148227e-04, 2.98909923e-03, 1.88269054e-03, 3.39307537e-03,
        2.77885613e-01],
       [4.71386886e-03, 4.78092896e-03, 5.42828241e-03, 3.83867225e-03,
        2.22150736e-01],
       ...,
       [7.92197108e-01, 8.11970141e-01, 7.90196475e-01, 8.15799920e-01,
        2.54672037e-02],
       [8.18777193e-01, 8.21510648e-01, 8.20249255e-01, 8.10219301e-01,
        1.70463908e-02],
       [8.19874096e-01, 8.19172449e-01, 8.12332341e-01, 8.09012935e-01,
        1.79975186e-02]])

As mentioned above we are going to train the model on data of 60 days at a time. So the code mentioned below divides the data into chunks of 60 rows. data_training.shape[0] is equal to 3617 which corresponds to the length of data_traning. After dividing we are converting X_train and y_train into numpy arrays.

X_train = []
y_train = []

for i in range(60, data_training.shape[0]):
    X_train.append(data_training[i-60:i])
    y_train.append(data_training[i, 0])
    
X_train, y_train = np.array(X_train), np.array(y_train)

As we can see X_train now consists of 3557 chunks of data having 60 lists each and each list has 5 elements which correspond to the 5 attributes in the dataset.

X_train.shape

(3557, 60, 5)

Building LSTM

Here we are importing the necessary layers to build out neural network

from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense, LSTM, Dropout

• The first layer is the LSTM layer with 60 units.
• We will be using relu activation function.
• The rectified linear activation function or ReLU for short is a piecewise linear function that will output the input directly if it is positive, otherwise, it will output zero.
• return_sequence when set to True returns the full sequence as the output.
• input_shape is set to (X_train.shape[1],5) which is (60,5)
• Dropout layer is used to by randomly set the outgoing edges of hidden units to 0 at each update of the training phase.
• The value passed in dropout specifies the probability at which outputs of the layer are dropped out.
• The last layer is the Dense layer is the regular deeply connected neural network layer.
• As we are predicting a single value the units in the last layer is set to 1.

regressor = Sequential()

regressor.add(LSTM(units = 60, activation = 'relu', return_sequences = True, input_shape = (X_train.shape[1], 5)))
regressor.add(Dropout(0.2))

regressor.add(LSTM(units = 60, activation = 'relu', return_sequences = True))
regressor.add(Dropout(0.2))

regressor.add(LSTM(units = 80, activation = 'relu', return_sequences = True))
regressor.add(Dropout(0.2))

regressor.add(LSTM(units = 120, activation = 'relu'))
regressor.add(Dropout(0.2))

regressor.add(Dense(units = 1))

regressor.summary()

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
lstm (LSTM)                  (None, 60, 60)            15840     
_________________________________________________________________
dropout (Dropout)            (None, 60, 60)            0         
_________________________________________________________________
lstm_1 (LSTM)                (None, 60, 60)            29040     
_________________________________________________________________
dropout_1 (Dropout)          (None, 60, 60)            0         
_________________________________________________________________
lstm_2 (LSTM)                (None, 60, 80)            45120     
_________________________________________________________________
dropout_2 (Dropout)          (None, 60, 80)            0         
_________________________________________________________________
lstm_3 (LSTM)                (None, 120)               96480     
_________________________________________________________________
dropout_3 (Dropout)          (None, 120)               0         
_________________________________________________________________
dense (Dense)                (None, 1)                 121       
=================================================================
Total params: 186,601
Trainable params: 186,601
Non-trainable params: 0
_________________________________________________________________

Here we are compiling the model and fitting it to the training data. We will use 50 epochs to train the model. An epoch is an iteration over the entire data provided. batch_size is the number of samples per gradient update i.e. here the weights will be updates after 32 training examples.

regressor.compile(optimizer='adam', loss = 'mean_squared_error')
regressor.fit(X_train, y_train, epochs=50, batch_size=32)

Train on 3557 samples

Epoch 45/50
3557/3557 [==============================] - 26s 7ms/sample - loss: 6.8088e-04
Epoch 46/50
3557/3557 [==============================] - 25s 7ms/sample - loss: 6.0968e-04
Epoch 47/50
3557/3557 [==============================] - 25s 7ms/sample - loss: 6.6604e-04
Epoch 48/50
3557/3557 [==============================] - 25s 7ms/sample - loss: 6.2150e-04
Epoch 49/50
3557/3557 [==============================] - 25s 7ms/sample - loss: 6.4292e-04
Epoch 50/50
3557/3557 [==============================] - 25s 7ms/sample - loss: 6.3066e-04

Prepare test dataset

These are the first 5 entries in the test data set. To predict opening on any day we need the data of previous 60 days.

data_test.head()

	Date	Open	High	Low	Close	Adj Close	Volume
3617	2019-01-02	1016.570007	1052.319946	1015.710022	1045.849976	1045.849976	1532600
3618	2019-01-03	1041.000000	1056.979980	1014.070007	1016.059998	1016.059998	1841100
3619	2019-01-04	1032.589966	1070.839966	1027.417969	1070.709961	1070.709961	2093900
3620	2019-01-07	1071.500000	1074.000000	1054.760010	1068.390015	1068.390015	1981900
3621	2019-01-08	1076.109985	1084.560059	1060.530029	1076.280029	1076.280029	1764900

past_60_days contains the data of the past 60 days required to predict the opening of the 1st day in the test data set.

past_60_days = data_training.tail(60)

We are going to append data_test to past_60_days and ignore the index of data_test and drop Date and Adj Close.

df = past_60_days.append(data_test, ignore_index = True)
df = df.drop(['Date', 'Adj Close'], axis = 1)
df.head()

	Open	High	Low	Close	Volume
0	1195.329956	1197.510010	1155.576050	1168.189941	2209500
1	1167.500000	1173.500000	1145.119995	1157.349976	1184300
2	1150.109985	1168.000000	1127.364014	1148.969971	1932400
3	1146.150024	1154.349976	1137.572021	1138.819946	1308700
4	1131.079956	1132.170044	1081.130005	1081.219971	2675700

Similar to the training data set we have to scale the test data so that all the values are in the range 0 to 1.

inputs = scaler.transform(df)
inputs

array([[0.93805611, 0.93755773, 0.92220906, 0.91781776, 0.0266752 ],
       [0.91527437, 0.91792904, 0.91350452, 0.90892169, 0.01425359],
       [0.90103881, 0.91343268, 0.89872289, 0.90204445, 0.02331778],
       ...,
       [0.93940683, 0.93712442, 0.93529076, 0.9247443 , 0.01947328],
       [0.92550693, 0.93064972, 0.92791493, 0.9339358 , 0.01954719],
       [0.93524016, 0.94894575, 0.95017564, 0.95130949, 0.01227612]])

We have to prepare the test data like the training data.

X_test = []
y_test = []

for i in range(60, inputs.shape[0]):
    X_test.append(inputs[i-60:i])
    y_test.append(inputs[i, 0])

X_test, y_test = np.array(X_test), np.array(y_test)
X_test.shape, y_test.shape

((192, 60, 5), (192,))

We are now going to predict the opening for X_test using predict()

y_pred = regressor.predict(X_test)

As we had scaled all the values down, now we will have to get them back to the original scale. scaler.scale_ gives the scaling level

scaler.scale_

array([8.18605127e-04, 8.17521128e-04, 8.32487534e-04, 8.20673293e-04,
       1.21162775e-08])

8.186 is the first value in the list which gives the scale of opening price. We will multiply y_pred and y_test with the inverse of this to get all the values to the original scale.

scale = 1/8.18605127e-04
scale

1221.5901990069017

y_pred = y_pred*scale
y_test = y_test*scale

Visualization

# Visualising the results
plt.figure(figsize=(14,5))
plt.plot(y_test, color = 'red', label = 'Real Google Stock Price')
plt.plot(y_pred, color = 'blue', label = 'Predicted Google Stock Price')
plt.title('Google Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('Google Stock Price')
plt.legend()
plt.show()

As we can see from the graph we have got a decent prediction of the opening price with a good accuracy.