Household Power Consumption Prediction using RNN-LSTM

Power outage accidents will cause huge economic loss to the social economy. Therefore, it is very important to predict power consumption.

Given the rise of smart electricity meters and the wide adoption of electricity generation technology like solar panels, there is a wealth of electricity usage data available.

---

Problem Statement :

Given that power consumption data for the previous week, we have to predict the power consumption for the next week.

Watch Full Video: 

Download dataset:

https://archive.ics.uci.edu/ml/machine-learning-databases/00235/household_power_consumption.zip

Details:

https://archive.ics.uci.edu/ml/datasets/individual+household+electric+power+consumption

Dataset Description:

The data was collected between December 2006 and November 2010 and observations of power consumption within the household were collected every minute.

It is a multivariate series comprised of seven variables

• global_active_power: The total active power consumed by the household (kilowatts).
• global_reactive_power: The total reactive power consumed by the household (kilowatts).
• voltage: Average voltage (volts).
• global_intensity: Average current intensity (amps).
• sub_metering_1: Active energy for kitchen (watt-hours of active energy).
• sub_metering_2: Active energy for laundry (watt-hours of active energy).
• sub_metering_3: Active energy for climate control systems (watt-hours of active energy).

This data represents a multivariate time series of power-related variables that in turn could be used to model and even forecast future electricity consumption

---

Time-series predictions play a major role in machine learning which is often neglected. Nonetheless, there are lots of machine learning algorithms we could use for these problems. The major machine learning algorithms involving Statsmodels and Econometric models etc. Today we will take a look at how to use and apply Deep learning algorithms to predict the time series Data

Why use a Deep Learning Algorithm?

With the data volume growing enormous day by day we shouldn’t confine ourselves to only the standard ML algorithms. Deep learning algorithms help us to handle large volumes of data and without leaving the key insights and by tuning the model within the right way gives us the maximum yield i.e., in our cause maximum accuracy 😊 . The model also determines if our prediction is better or worse from its own neural network architecture.

For this Time series forecasting we will use Long- Short Term Memory unit (LSTM).

Recurrent Neural Network (RNN)

To understand an LSTM Network, we need to understand a Recurrent Neural Network first. This kind of network is used to recognize patterns when past results have influence on the present result. An example of RNN usage is the time-series functions, in which the data order is extremely important. In this network architecture, the neuron uses as input not only the regular input (the previous layer output), but also its previous state.

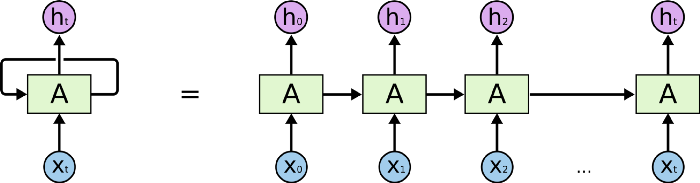
It is important to notice that H represents the neuron state. Therefore, when in state H_1, the neuron uses as input the parameter X_1 and H_0 (its previous state). The main problem of this model is the memory loss. The network older states are fast forgotten. In sequences where we need to remember beyond the immediate past, RNNs fail to remember.

Long Short Term Memory unit(LSTM) was typically created to overcome the limitations of a Recurrent neural network (RNN). The Typical long data sets of Time series can actually be a time-consuming process which could typically slow down the training time of RNN architecture. We could restrict the data volume but this a loss of information. And in any time-series data sets, there is a need to know the previous trends and the seasonality of data of the overall data set to make the right predictions.

Before going into the brief explanation of LSTM cell, Let us see how the LSTM cell looks like :

The Architecture may look little complicated on the first glance, but it is pretty neat and clear and easily understandable if we break it into parts.

Lets first start understanding what are our inputs and outputs. The typical input if you see on the left-hand side of the diagram Ct-1 which is the previous cell state and ht-1 which is the output from the previous cell and Xt which is the input of the present cell.

The output of the cell is Ct and ht which are the corresponding cell state and output of the present cell. The first step of an LSTM is the forget gate layer (f) where we determine what are we going to forget from the previous cell state. This typically takes the input ht-1 and Xt and make a linear transformation with some weights and bias terms and pass into the sigmoid function. As we are aware the output of a sigmoid function is always between 0 and 1. Here 0 will be considered as to forget it and 1 will represent to keep it

Forget gate later=> f = Sigmoid ( Weights (ht-1,Xt) + bias)

The second step is a two-part process and this is the step which tells us actually processing within this layer. Here in the first part we take the same inputs as before the ht-1 and Xt and make a linear transformation with some weights and biases and pass on to a sigmoid function. And the second part we will make a linear transformation again between ht-1 and Xt with some weights and biases but this time its going to be a hyperbolic tangent function (tanh). At the end of this step, we will get vectors of values which can be new candidate values for this present cell.

First part => I = sigmoid( Weights (ht-1,Xt) + bias)

Second part => II = tanh( Weights (ht-1,Xt) + bias)

The third step is the update step which helps us in deriving the new cell state Ct using our previous steps. First, we will multiply the previous cell state with the forget gate layer and add the vectors we got from the second step which forms the new cell state Ct of the present cell at t.

Update layer => Ct = Ct-1 f + I II

The final step is another main output of the cell, for this, we will directly form a linear transformation with the previous output ht-1 and input of the present cell Xt with some bias and weight terms and pass on to a sigmoid layer. Finally, now we will multiply this output to the new cell state Ct which is passed on to a hyperbolic tangent function. This gives us the present output ht.

Final layer =>

i = sigmoid ( Weights (ht-1,xt) + bias)

final ht = i * tanh(Ct)

Now we have a clear understanding of the step by step dissection of the LSTM layer. Let's see how we apply our LSTM cell into a time series data.

How to? Let's Begin

Importing Libraries

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from numpy import nan

from tensorflow.keras import Sequential
from tensorflow.keras.layers import LSTM, Dense

from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScaler

#Reading the dataset

data = pd.read_csv('household_power_consumption.txt', sep = ';',
                  parse_dates = True,
                  low_memory = False)

#printing top rows

data.head()

	Date	Time	Global_active_power	Global_reactive_power	Voltage	Global_intensity	Sub_metering_1	Sub_metering_2	Sub_metering_3
0	16/12/2006	17:24:00	4.216	0.418	234.840	18.400	0.000	1.000	17.0
1	16/12/2006	17:25:00	5.360	0.436	233.630	23.000	0.000	1.000	16.0
2	16/12/2006	17:26:00	5.374	0.498	233.290	23.000	0.000	2.000	17.0
3	16/12/2006	17:27:00	5.388	0.502	233.740	23.000	0.000	1.000	17.0
4	16/12/2006	17:28:00	3.666	0.528	235.680	15.800	0.000	1.000	17.0

#concatenating the date and time columns to 'date_time' columns

data['date_time'] = data['Date'].str.cat(data['Time'], sep= ' ')
data.drop(['Date', 'Time'], inplace= True, axis = 1)
data.head()

	Global_active_power	Global_reactive_power	Voltage	Global_intensity	Sub_metering_1	Sub_metering_2	Sub_metering_3	date_time
0	4.216	0.418	234.840	18.400	0.000	1.000	17.0	16/12/2006 17:24:00
1	5.360	0.436	233.630	23.000	0.000	1.000	16.0	16/12/2006 17:25:00
2	5.374	0.498	233.290	23.000	0.000	2.000	17.0	16/12/2006 17:26:00
3	5.388	0.502	233.740	23.000	0.000	1.000	17.0	16/12/2006 17:27:00
4	3.666	0.528	235.680	15.800	0.000	1.000	17.0	16/12/2006 17:28:00

data.set_index(['date_time'], inplace=True)
data.head()

	Global_active_power	Global_reactive_power	Voltage	Global_intensity	Sub_metering_1	Sub_metering_2	Sub_metering_3
date_time
16/12/2006 17:24:00	4.216	0.418	234.840	18.400	0.000	1.000	17.0
16/12/2006 17:25:00	5.360	0.436	233.630	23.000	0.000	1.000	16.0
16/12/2006 17:26:00	5.374	0.498	233.290	23.000	0.000	2.000	17.0
16/12/2006 17:27:00	5.388	0.502	233.740	23.000	0.000	1.000	17.0
16/12/2006 17:28:00	3.666	0.528	235.680	15.800	0.000	1.000	17.0

Next, we can mark all missing values indicated with a ‘?‘ character with a NaN value, which is a float.

#replacing each '?'characters with NaN value

data.replace('?', nan, inplace=True)

#This will allow us to work with the data as one array of floating point values rather than mixed types (less efficient.)

data = data.astype('float')

#information of the dataset

data.info()

<class 'pandas.core.frame.DataFrame'>
Index: 2075259 entries, 16/12/2006 17:24:00 to 26/11/2010 21:02:00
Data columns (total 7 columns):
Global_active_power      float64
Global_reactive_power    float64
Voltage                  float64
Global_intensity         float64
Sub_metering_1           float64
Sub_metering_2           float64
Sub_metering_3           float64
dtypes: float64(7)
memory usage: 126.7+ MB

#checking the null values

np.isnan(data).sum()

Global_active_power      25979
Global_reactive_power    25979
Voltage                  25979
Global_intensity         25979
Sub_metering_1           25979
Sub_metering_2           25979
Sub_metering_3           25979
dtype: int64

We also need to fill in the missing values now that they have been marked.

A very simple approach would be to copy the observation from the same time the day before. We can implement this in a function named fill_missing() that will take the NumPy array of the data and copy values from exactly 24 hours ago.

def fill_missing(data):
    one_day = 24*60
    for row in range(data.shape[0]):
        for col in range(data.shape[1]):
            if np.isnan(data[row, col]):
                data[row, col] = data[row-one_day, col]

fill_missing(data.values)

#checking the nan values

np.isnan(data).sum()

Global_active_power      0
Global_reactive_power    0
Voltage                  0
Global_intensity         0
Sub_metering_1           0
Sub_metering_2           0
Sub_metering_3           0
dtype: int64

data.info()

<class 'pandas.core.frame.DataFrame'>
Index: 2075259 entries, 16/12/2006 17:24:00 to 26/11/2010 21:02:00
Data columns (total 7 columns):
Global_active_power      float64
Global_reactive_power    float64
Voltage                  float64
Global_intensity         float64
Sub_metering_1           float64
Sub_metering_2           float64
Sub_metering_3           float64
dtypes: float64(7)
memory usage: 126.7+ MB

#printing the shape of the data

data.shape

(2075259, 7)

Here, we can observe that we have 2075259 datapoints and 7 features

data.head()

	Global_active_power	Global_reactive_power	Voltage	Global_intensity	Sub_metering_1	Sub_metering_2	Sub_metering_3
date_time
16/12/2006 17:24:00	4.216	0.418	234.84	18.4	0.0	1.0	17.0
16/12/2006 17:25:00	5.360	0.436	233.63	23.0	0.0	1.0	16.0
16/12/2006 17:26:00	5.374	0.498	233.29	23.0	0.0	2.0	17.0
16/12/2006 17:27:00	5.388	0.502	233.74	23.0	0.0	1.0	17.0
16/12/2006 17:28:00	3.666	0.528	235.68	15.8	0.0	1.0	17.0

Prepare power consumption for each day

We can now save the cleaned-up version of the dataset to a new file; in this case we will just change the file extension to .csv and save the dataset as ‘cleaned_data.csv‘.

#conversion of dataframe to .csv

data.to_csv('cleaned_data.csv')

#reading the dataset

dataset = pd.read_csv('cleaned_data.csv', parse_dates = True, index_col = 'date_time', low_memory = False)

#printing the top rows

dataset.head()

	Global_active_power	Global_reactive_power	Voltage	Global_intensity	Sub_metering_1	Sub_metering_2	Sub_metering_3
date_time
2006-12-16 17:24:00	4.216	0.418	234.84	18.4	0.0	1.0	17.0
2006-12-16 17:25:00	5.360	0.436	233.63	23.0	0.0	1.0	16.0
2006-12-16 17:26:00	5.374	0.498	233.29	23.0	0.0	2.0	17.0
2006-12-16 17:27:00	5.388	0.502	233.74	23.0	0.0	1.0	17.0
2006-12-16 17:28:00	3.666	0.528	235.68	15.8	0.0	1.0	17.0

#printing the bottom rows

dataset.tail()

	Global_active_power	Global_reactive_power	Voltage	Global_intensity	Sub_metering_1	Sub_metering_2	Sub_metering_3
date_time
2010-11-26 20:58:00	0.946	0.0	240.43	4.0	0.0	0.0	0.0
2010-11-26 20:59:00	0.944	0.0	240.00	4.0	0.0	0.0	0.0
2010-11-26 21:00:00	0.938	0.0	239.82	3.8	0.0	0.0	0.0
2010-11-26 21:01:00	0.934	0.0	239.70	3.8	0.0	0.0	0.0
2010-11-26 21:02:00	0.932	0.0	239.55	3.8	0.0	0.0	0.0

Exploratory Data Analysis

#Downsampling the data into dáy-wise bins and sum the values of the timestamps falling into a bin.

data = dataset.resample('D').sum()

#data after sampling it into daywise manner

data.head()

	Global_active_power	Global_reactive_power	Voltage	Global_intensity	Sub_metering_1	Sub_metering_2	Sub_metering_3
date_time
2006-12-16	1209.176	34.922	93552.53	5180.8	0.0	546.0	4926.0
2006-12-17	3390.460	226.006	345725.32	14398.6	2033.0	4187.0	13341.0
2006-12-18	2203.826	161.792	347373.64	9247.2	1063.0	2621.0	14018.0
2006-12-19	1666.194	150.942	348479.01	7094.0	839.0	7602.0	6197.0
2006-12-20	2225.748	160.998	348923.61	9313.0	0.0	2648.0	14063.0

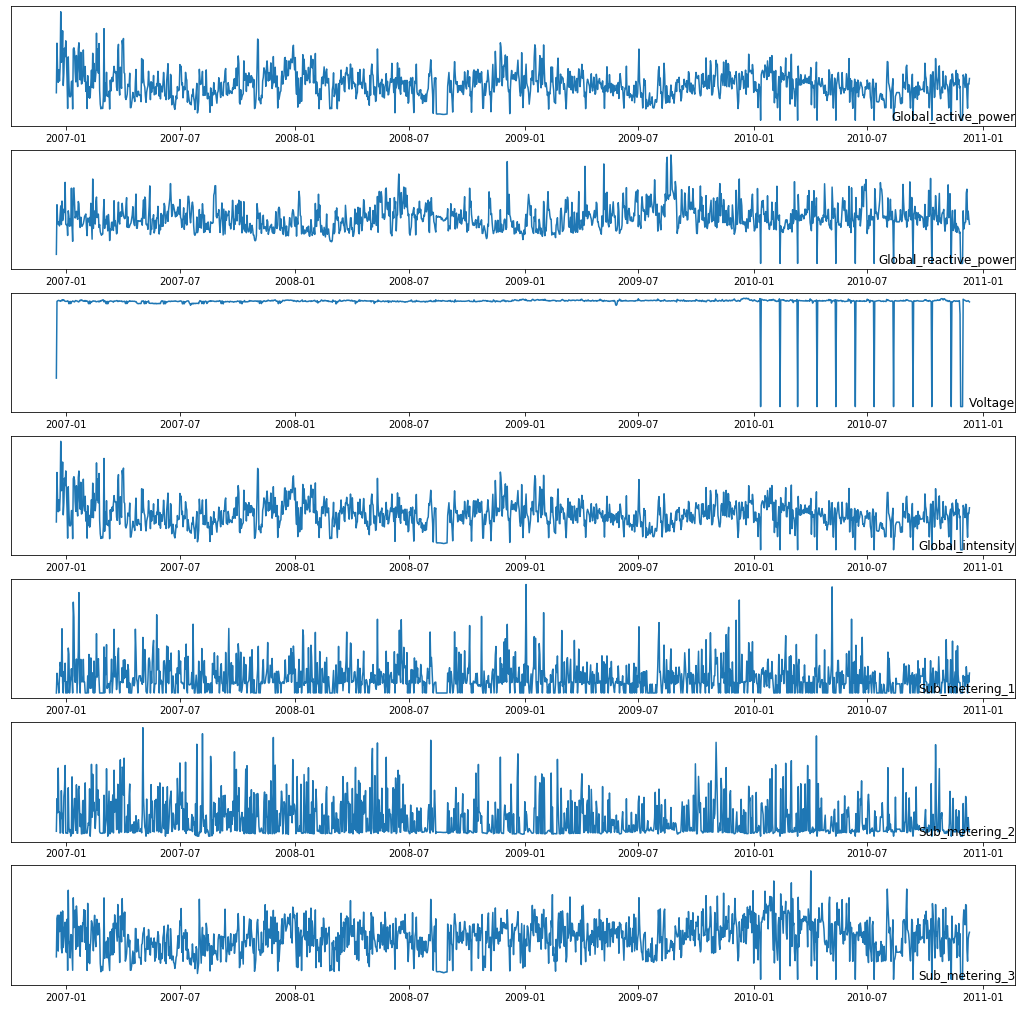
Plotting the all features in various time stamps

fig, ax = plt.subplots(figsize=(18,18))

for i in range(len(data.columns)):
    plt.subplot(len(data.columns), 1, i+1)
    name = data.columns[i]
    plt.plot(data[name])
    plt.title(name, y=0, loc = 'right')
    plt.yticks([])
plt.show()
fig.tight_layout()

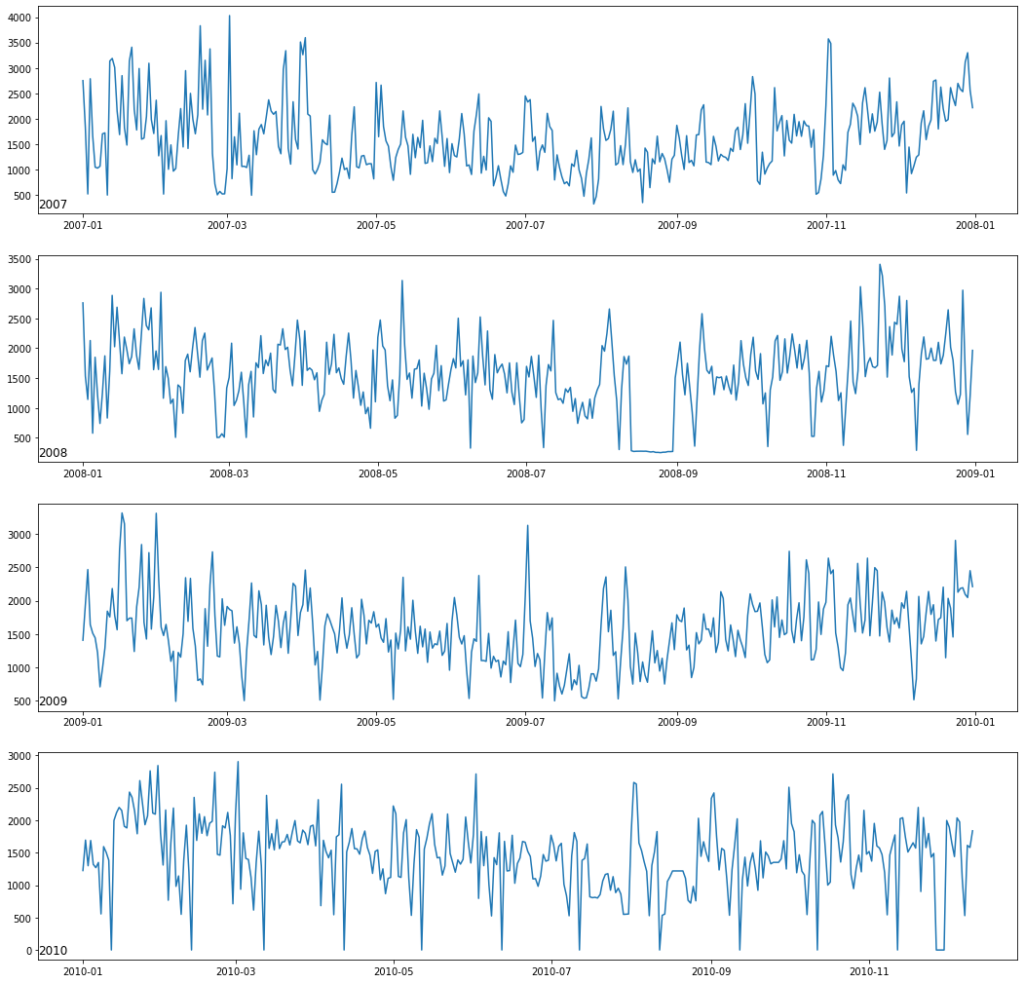
Exploring Active power consumption for each year

#we have considered 5 years here

years = ['2007', '2008', '2009', '2010']

Year wise plotting of feature Global_active_power

fig, ax = plt.subplots(figsize=(18,18))

for i in range(len(years)):
    plt.subplot(len(years), 1, i+1)
    year = years[i]
    active_power_data = data[str(year)]
    plt.plot(active_power_data['Global_active_power'])
    plt.title(str(year), y = 0, loc = 'left')
plt.show()
fig.tight_layout()

#for year 2006

data['2006']

	Global_active_power	Global_reactive_power	Voltage	Global_intensity	Sub_metering_1	Sub_metering_2	Sub_metering_3
date_time
2006-12-16	1209.176	34.922	93552.53	5180.8	0.0	546.0	4926.0
2006-12-17	3390.460	226.006	345725.32	14398.6	2033.0	4187.0	13341.0
2006-12-18	2203.826	161.792	347373.64	9247.2	1063.0	2621.0	14018.0
2006-12-19	1666.194	150.942	348479.01	7094.0	839.0	7602.0	6197.0
2006-12-20	2225.748	160.998	348923.61	9313.0	0.0	2648.0	14063.0
2006-12-21	1723.288	144.434	347096.41	7266.4	1765.0	2692.0	10456.0
2006-12-22	2341.338	186.906	347305.75	9897.0	3151.0	350.0	11131.0
2006-12-23	4773.386	221.470	345795.95	20200.4	2669.0	425.0	14726.0
2006-12-24	2550.012	149.900	348029.91	11002.2	1703.0	5082.0	6891.0
2006-12-25	2743.120	240.280	350495.90	11450.2	6620.0	1962.0	5795.0
2006-12-26	3934.110	165.102	347940.63	16341.0	1086.0	2533.0	14979.0
2006-12-27	1528.760	178.902	351025.00	6505.2	0.0	314.0	6976.0
2006-12-28	2072.638	208.876	350306.40	8764.2	2207.0	4419.0	9176.0
2006-12-29	3174.392	196.394	346854.68	13350.8	1252.0	5162.0	11329.0
2006-12-30	2796.108	312.142	346377.15	11952.6	3072.0	7893.0	12516.0
2006-12-31	3494.196	150.852	345451.07	14687.4	0.0	347.0	6502.0

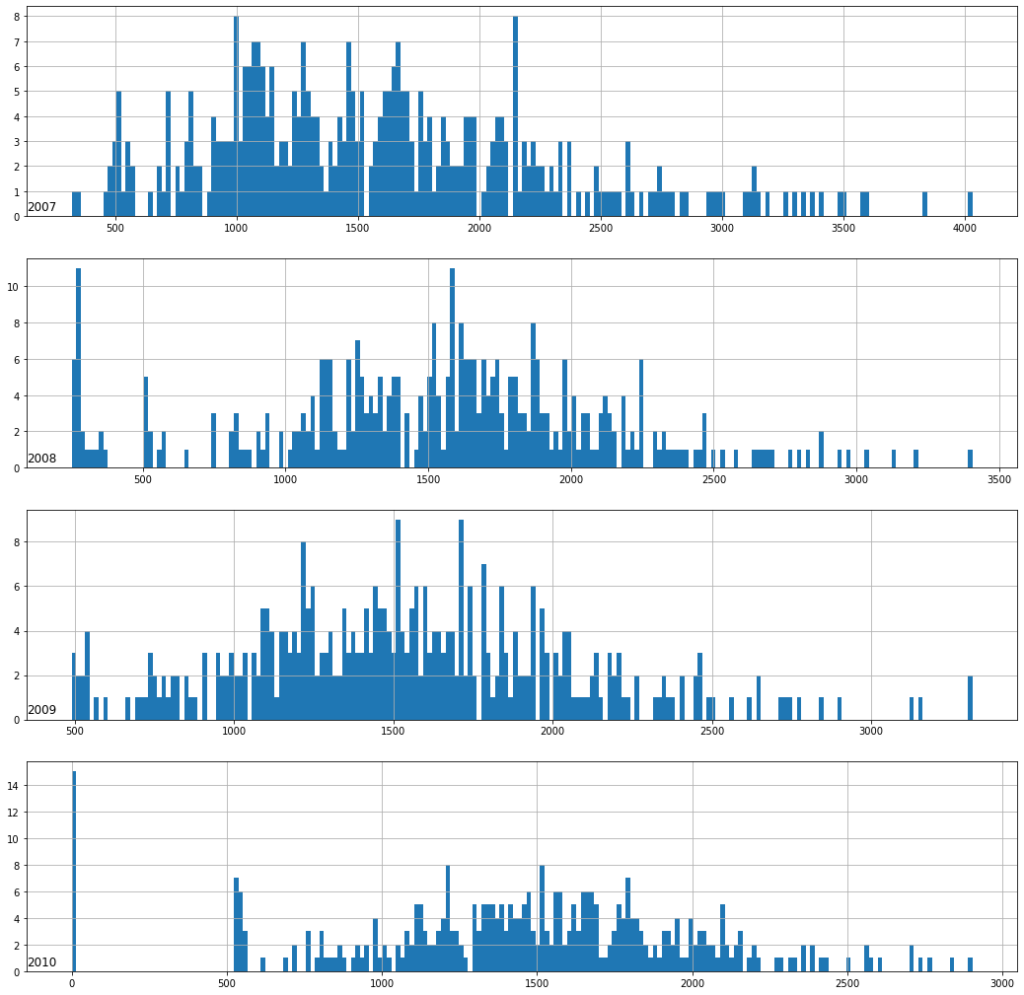
Power consumption distribution with histogram

Year wise histogram plot of feature Global_active_power

fig, ax = plt.subplots(figsize=(18,18))

for i in range(len(years)):
    plt.subplot(len(years), 1, i+1)
    year = years[i]
    active_power_data = data[str(year)]
    active_power_data['Global_active_power'].hist(bins = 200)
    plt.title(str(year), y = 0, loc = 'left')
plt.show()
fig.tight_layout()

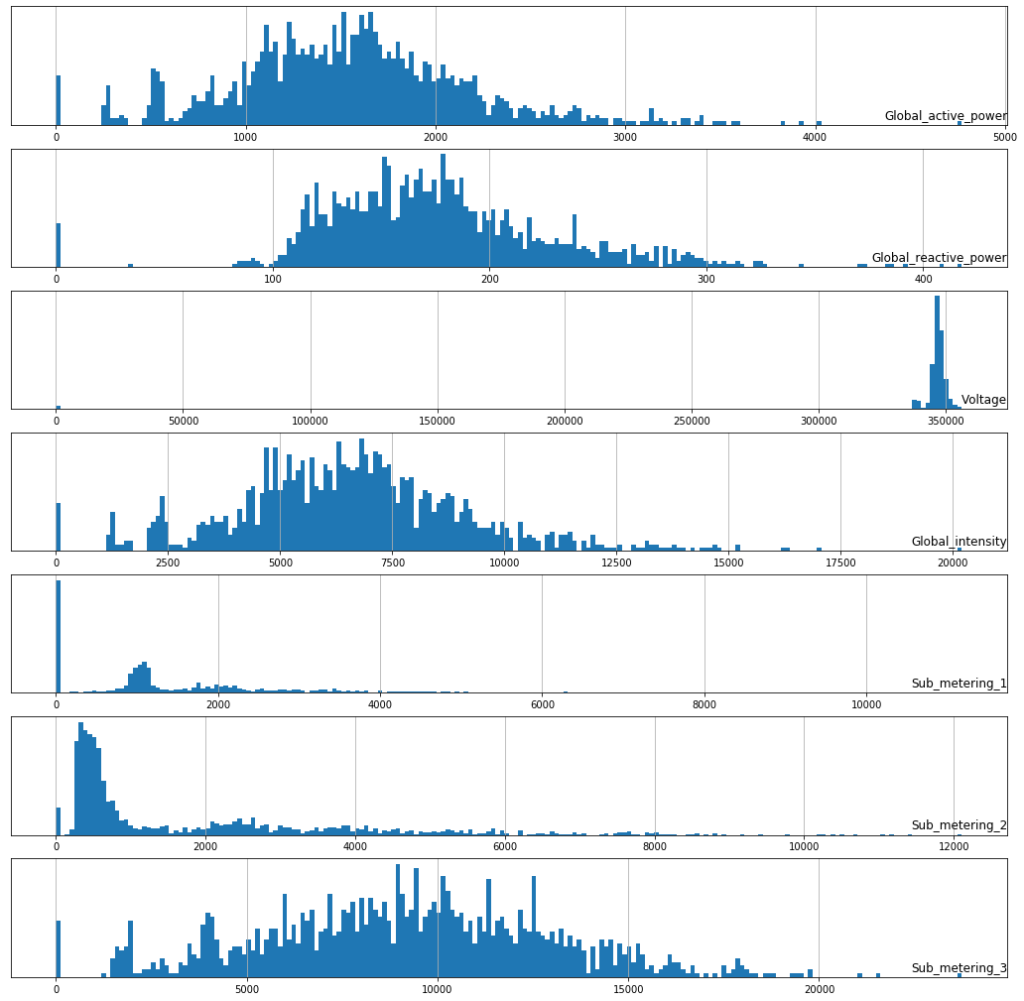
Histogram plot for All Features

fig, ax = plt.subplots(figsize=(18,18))

for i in range(len(data.columns)):
    plt.subplot(len(data.columns), 1, i+1)
    name = data.columns[i]
    data[name].hist(bins=200)
    plt.title(name, y=0, loc = 'right')
    plt.yticks([])
plt.show()
fig.tight_layout()

Plot power consumption hist for each month of 2007

months = [i for i in range(1,13)]

fig, ax = plt.subplots(figsize=(18,18))

for i in range(len(months)):
    ax = plt.subplot(len(months), 1, i+1)
    month = '2007-' + str(months[i])
    active_power_data = dataset[month]
    active_power_data['Global_active_power'].hist(bins = 100)
    ax.set_xlim(0,5)
    plt.title(month, y = 0, loc = 'right')
plt.show()
fig.tight_layout()

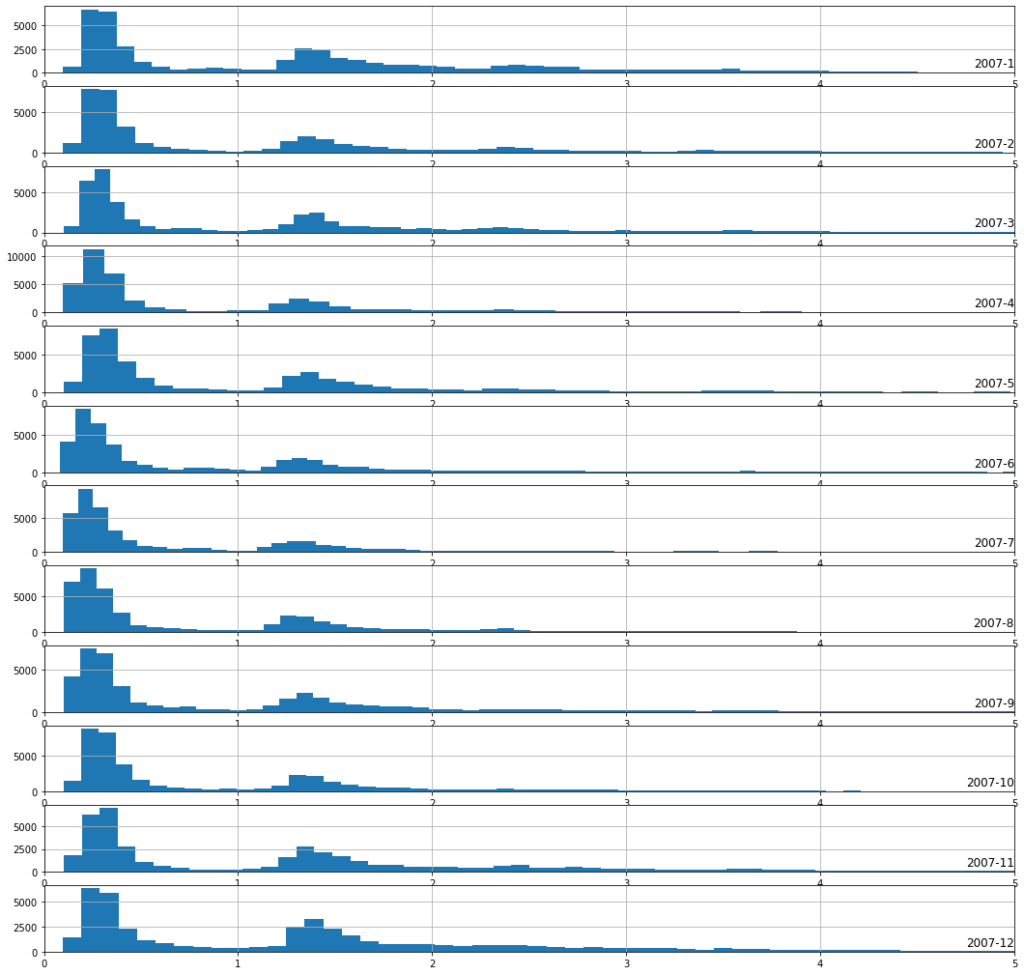
Observation :

1. From the above diagram we can say that power consumption in the month of Nov, Dec, Jan, Feb, Mar is more as there is a long tail as compare to other months.

2. It also shows that the during the winter seasons, the heating systems are used and not in summer.

3. The above graph is highly concentrated on 0.3W and 1.3W.

Active Power Uses Prediction

What can we predict

• Forecast hourly consumption for the next day.
• Forecast daily consumption for the next week.
• Forecast daily consumption for the next month.
• Forecast monthly consumption for the next year.

Modeling Methods

There are many modeling methods and few of those are as follows

• Naive Methods -> Naive methods would include methods that make very simple, but often very effective assumptions.
• Classical Linear Methods -> Classical linear methods include techniques are very effective for univariate time series forecasting
• Machine Learning Methods -> Machine learning methods require that the problem be framed as a supervised learning problem.
  • K-nearest neighbors.
  • SVM
  • Decision trees
  • Random forest
  • Gradient boosting machines
• Deep Learning Methods -> combinations of CNN LSTM and ConvLSTM, have proven effective on time series classification tasks
  • CNN
  • LSTM
  • CNN - LSTM

---

Problem Framing:

Given recent power consumption, what is the expected power consumption for the week ahead?

This requires that a predictive model forecast the total active power for each day over the next seven days

A model of this type could be helpful within the household in planning expenditures. It could also be helpful on the supply side for planning electricity demand for a specific household.

Input -> Predict

[Week1] -> Week2

[Week2] -> Week3

[Week3] -> Week4

#top rows

data.head()

	Global_active_power	Global_reactive_power	Voltage	Global_intensity	Sub_metering_1	Sub_metering_2	Sub_metering_3
date_time
2006-12-16	1209.176	34.922	93552.53	5180.8	0.0	546.0	4926.0
2006-12-17	3390.460	226.006	345725.32	14398.6	2033.0	4187.0	13341.0
2006-12-18	2203.826	161.792	347373.64	9247.2	1063.0	2621.0	14018.0
2006-12-19	1666.194	150.942	348479.01	7094.0	839.0	7602.0	6197.0
2006-12-20	2225.748	160.998	348923.61	9313.0	0.0	2648.0	14063.0

#printing last rows

data.tail()

	Global_active_power	Global_reactive_power	Voltage	Global_intensity	Sub_metering_1	Sub_metering_2	Sub_metering_3
date_time
2010-12-07	1109.574	285.912	345914.85	4892.0	1724.0	646.0	6444.0
2010-12-08	529.698	169.098	346744.70	2338.2	0.0	514.0	3982.0
2010-12-09	1612.092	201.358	347932.40	6848.2	1805.0	2080.0	8891.0
2010-12-10	1579.692	170.268	345975.37	6741.2	1104.0	780.0	9812.0
2010-12-11	1836.822	151.144	343926.57	7826.2	2054.0	489.0	10308.0

#here are splitting the dataset
#dataset upto end of 2009 is in train dataset and remaining we keeping it in test dataset

data_train = data.loc[:'2009-12-31', :]['Global_active_power']
data_train.head()

date_time
2006-12-16    1209.176
2006-12-17    3390.460
2006-12-18    2203.826
2006-12-19    1666.194
2006-12-20    2225.748
Freq: D, Name: Global_active_power, dtype: float64

data_test = data['2010']['Global_active_power']
data_test.head()

date_time
2010-01-01    1224.252
2010-01-02    1693.778
2010-01-03    1298.728
2010-01-04    1687.440
2010-01-05    1320.158
Freq: D, Name: Global_active_power, dtype: float64

data_train.shape

(1112,)

data_test.shape

(345,)

Observation :

1. We have 1112 datapoints in train dataset and 345 datapoints in test dataset

Prepare training data

#training data

data_train.head(14)

date_time
2006-12-16    1209.176
2006-12-17    3390.460
2006-12-18    2203.826
2006-12-19    1666.194
2006-12-20    2225.748
2006-12-21    1723.288
2006-12-22    2341.338
2006-12-23    4773.386
2006-12-24    2550.012
2006-12-25    2743.120
2006-12-26    3934.110
2006-12-27    1528.760
2006-12-28    2072.638
2006-12-29    3174.392
Freq: D, Name: Global_active_power, dtype: float64

#converting the data into numpy array

data_train = np.array(data_train)

#we are splitting the data weekly wise(7days)

X_train, y_train = [], []

for i in range(7, len(data_train)-7):
    X_train.append(data_train[i-7:i])
    y_train.append(data_train[i:i+7])

#converting list to numpy array

X_train, y_train = np.array(X_train), np.array(y_train)

#shape of train and test dataset

X_train.shape, y_train.shape

((1098, 7), (1098, 7))

#printing the ytrain value

pd.DataFrame(y_train).head()

	0	1	2	3	4	5	6
0	4773.386	2550.012	2743.120	3934.110	1528.760	2072.638	3174.392
1	2550.012	2743.120	3934.110	1528.760	2072.638	3174.392	2796.108
2	2743.120	3934.110	1528.760	2072.638	3174.392	2796.108	3494.196
3	3934.110	1528.760	2072.638	3174.392	2796.108	3494.196	2749.004
4	1528.760	2072.638	3174.392	2796.108	3494.196	2749.004	1824.760

#Normalising the dataset between 0 and 1

x_scaler = MinMaxScaler()
X_train = x_scaler.fit_transform(X_train)

#Normalising the dataset

y_scaler = MinMaxScaler()
y_train = y_scaler.fit_transform(y_train)

pd.DataFrame(X_train).head()

	0	1	2	3	4	5	6
0	0.211996	0.694252	0.431901	0.313037	0.436748	0.325660	0.462304
1	0.694252	0.431901	0.313037	0.436748	0.325660	0.462304	1.000000
2	0.431901	0.313037	0.436748	0.325660	0.462304	1.000000	0.508439
3	0.313037	0.436748	0.325660	0.462304	1.000000	0.508439	0.551133
4	0.436748	0.325660	0.462304	1.000000	0.508439	0.551133	0.814446

#converting to 3 dimension

X_train = X_train.reshape(1098, 7, 1)

X_train.shape

(1098, 7, 1)

Build LSTM Model

#building sequential model using Keras

reg = Sequential()
reg.add(LSTM(units = 200, activation = 'relu', input_shape=(7,1)))
reg.add(Dense(7))

#here we have considered loss as mean square error and optimizer as adam

reg.compile(loss='mse', optimizer='adam')

#training the model

reg.fit(X_train, y_train, epochs = 100)

Train on 1098 samples
Epoch 1/100
1098/1098 [==============================] - 2s 2ms/sample - loss: 0.0626
Epoch 2/100
1098/1098 [==============================] - 0s 296us/sample - 
.
.
.
.
.
Epoch 99/100
1098/1098 [==============================] - 0s 270us/sample - loss: 0.0228
Epoch 100/100
1098/1098 [==============================] - 0s 269us/sample - loss: 0.0228

<tensorflow.python.keras.callbacks.History at 0x19ba56fc668>

Observation:

1. We have done with training and loss which we have got is 0.0232

Prepare test dataset and test LSTM model

#testing dataset

data_test = np.array(data_test)

#here we are splitting the data weekly wise(7days)

X_test, y_test = [], []

for i in range(7, len(data_test)-7):
    X_test.append(data_test[i-7:i])
    y_test.append(data_test[i:i+7])

X_test, y_test = np.array(X_test), np.array(y_test)

X_test = x_scaler.transform(X_test)
y_test = y_scaler.transform(y_test)

#converting to 3 dimension

X_test = X_test.reshape(331,7,1)

X_test.shape

(331, 7, 1)

y_pred = reg.predict(X_test)

#bringing y_pred values to their original forms by using inverse transform

y_pred = y_scaler.inverse_transform(y_pred)

y_pred

array([[1508.9413 , 1476.1537 , 1487.5676 , ..., 1484.8464 , 1459.3864 ,
        1551.5675 ],
       [1158.2788 , 1287.0326 , 1346.428  , ..., 1430.5685 , 1420.6346 ,
        1472.5759 ],
       [1571.7665 , 1507.0337 , 1516.5574 , ..., 1432.5813 , 1393.9161 ,
        1504.1714 ],
       ...,
       [ 952.85785,  852.4236 ,  933.62585, ...,  800.12006,  831.2844 ,
        1005.20844],
       [1579.4896 , 1353.6078 , 1278.9501 , ...,  981.4198 ,  967.6466 ,
        1146.7898 ],
       [1629.0509 , 1392.7751 , 1288.7218 , ..., 1052.977  , 1070.8586 ,
        1243.1346 ]], dtype=float32)

y_true = y_scaler.inverse_transform(y_test)

y_true

array([[ 555.664, 1593.318, 1504.82 , ...,    0.   , 1995.796, 2116.224],
       [1593.318, 1504.82 , 1383.18 , ..., 1995.796, 2116.224, 2196.76 ],
       [1504.82 , 1383.18 ,    0.   , ..., 2116.224, 2196.76 , 2150.112],
       ...,
       [1892.998, 1645.424, 1439.426, ..., 1973.382, 1109.574,  529.698],
       [1645.424, 1439.426, 2035.418, ..., 1109.574,  529.698, 1612.092],
       [1439.426, 2035.418, 1973.382, ...,  529.698, 1612.092, 1579.692]])

Evaluate the model

Here, we using metric as mean square error since it is a regression problem

def evaluate_model(y_true, y_predicted):
    scores = []
    
    #calculate scores for each day
    for i in range(y_true.shape[1]):
        mse = mean_squared_error(y_true[:, i], y_predicted[:, i])
        rmse = np.sqrt(mse)
        scores.append(rmse)
    
    #calculate score for whole prediction
    total_score = 0
    for row in range(y_true.shape[0]):
        for col in range(y_predicted.shape[1]):
            total_score = total_score + (y_true[row, col] - y_predicted[row, col])**2
    total_score = np.sqrt(total_score/(y_true.shape[0]*y_predicted.shape[1]))
    
    return total_score, scores

evaluate_model(y_true, y_pred)

(579.2827596682928,
 [598.0411885086157,
  592.5770673397814,
  576.1153945912635,
  563.9396525162248,
  576.5479538079353,
  570.7699415990154,
  576.2430188855649])

#standard deviation

np.std(y_true[0])

710.0253857243853

Conclusions:

1. From the above experiment, we have got root mean square error around 598 watts.
2. In order to check whether our model is performing good or bad, we need to evaluate standard deviation which we have got here as 710 watts.
3. Here mean square error is less than standard deviation. Hence, we can say that our model is performing good.

---