Feature Dimension Reduction

Watch Full Playlist: https://www.youtube.com/playlist?list=PLc2rvfiptPSQYzmDIFuq2PqN2n28ZjxDH

What is LDA (Linear Discriminant Analysis)?

The idea behind LDA is simple. Mathematically speaking, we need to find a new feature space to project the data in order to maximize classes separability

Linear Discriminant Analysis is a supervised algorithm as it takes the class label into consideration. It is a way to reduce ‘dimensionality’ while at the same time preserving as much of the class discrimination information as possible.

LDA helps you find the boundaries around clusters of classes. It projects your data points on a line so that your clusters are as separated as possible, with each cluster having a relative (close) distance to a centroid.

So the question arises- how are these clusters are defined and how do we get the reduced feature set in case of LDA?

Basically LDA finds a centroid of each class datapoints. For example with thirteen different features LDA will find the centroid of each of its class using the thirteen different feature dataset. Now on the basis of this, it determines a new dimension which is nothing but an axis which should satisfy two criteria:

1. Maximize the distance between the centroid of each class.
2. Minimize the variation (which LDA calls scatter and is represented by s2), within each category.

What is PCA

Principal Component Analysis (PCA) is a linear dimensionality reduction technique that can be utilized for extracting information from a high-dimensional space by projecting it into a lower-dimensional sub-space. It tries to preserve the essential parts that have more variation of the data and remove the non-essential parts with fewer variation.

Dimensions are nothing but features that represent the data. For example, A 28 X 28 image has 784 picture elements (pixels) that are the dimensions or features which together represent that image.

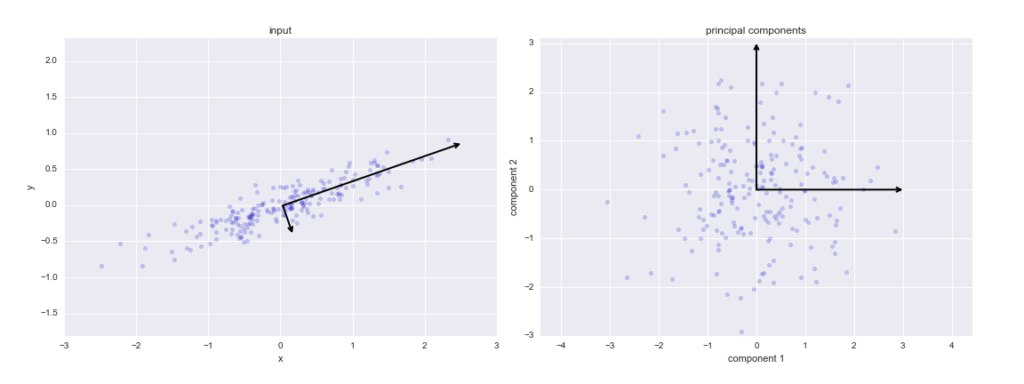
One important thing to note about PCA is that it is an Unsupervised dimensionality reduction technique, you can cluster the similar data points based on the feature correlation between them without any supervision (or labels), and you will learn how to achieve this practically using Python in later sections of this tutorial!

According to Wikipedia, PCA is a statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables (entities each of which takes on various numerical values) into a set of values of linearly uncorrelated variables called principal components.

When to use PCA

Data Visualization:
When working on any data related problem, the challenge in today's world is the sheer volume of data, and the variables/features that define that data. To solve a problem where data is the key, you need extensive data exploration like finding out how the variables are correlated or understanding the distribution of a few variables. Considering that there are a large number of variables or dimensions along which the data is distributed, visualization can be a challenge and almost impossible.

Speeding Machine Learning (ML) Algorithm:
Since PCA's main idea is dimensionality reduction, you can leverage that to speed up your machine learning algorithm's training and testing time considering your data has a lot of features, and the ML algorithm's learning is too slow.

How to do PCA

We can calculate a Principal Component Analysis on a dataset using the PCA() class in the scikit-learn library. The benefit of this approach is that once theprojection is calculated, it can be applied to new data again and again quite easily.

When creating the class, the number of components can be specified as a parameter.

The class is first fit on a dataset by calling the fit() function, and then the original dataset or other data can be projected into a subspace with the chosen number of dimensions by calling the transform() function.

Once fit, the eigenvalues and principal components can be accessed on the PCA class via the explainedvariance and components_ attributes.

Let's go ahead and learn with the script.

Importing required libraries

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline

from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, roc_auc_score
from sklearn.feature_selection import VarianceThreshold
from sklearn.preprocessing import StandardScaler

Here, we are going to read the santander data into variable data.

data = pd.read_csv('santander.csv', nrows = 20000)
data.head()

Let's read this into the x and y vectors to train .

X = data.drop('TARGET', axis = 1)
y = data['TARGET']
X.shape, y.shape

((20000, 370), (20000,))

Now, we will split the dataset into train and test datasets, you can observe from the following script.

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0, stratify = y)

Remove Constant, Quasi Constant and Duplicate Features

Let's remove constant and quasi constant features from the data with the threshold value of 0.01. That means the features which have 99% similarity among them have been removed.

constant_filter = VarianceThreshold(threshold=0.01)
constant_filter.fit(X_train)
X_train_filter = constant_filter.transform(X_train)
X_test_filter = constant_filter.transform(X_test)
X_train_filter.shape, X_test_filter.shape

((16000, 245), (4000, 245))

Let's remove duplicated features from the data.

X_train_T = X_train_filter.T
X_test_T = X_test_filter.T
X_train_T = pd.DataFrame(X_train_T)
X_test_T =pd.DataFrame(X_test_T)X_train_T.duplicated().sum()

18

duplicated_features = X_train_T.duplicated()
features_to_keep = [not index for index in duplicated_features]
X_train_unique = X_train_T[features_to_keep].T
X_test_unique = X_test_T[features_to_keep].T

Let's go ahead and standardize the data to get the same scale.

scaler = StandardScaler().fit(X_train_unique)
X_train_unique = scaler.transform(X_train_unique)
X_test_unique = scaler.transform(X_test_unique)
X_train_unique = pd.DataFrame(X_train_unique)
X_test_unique = pd.DataFrame(X_test_unique)X_train_unique.shape, X_test_unique.shape

((16000, 227), (4000, 227))

Removal of correlated Feature

Now we will find out the correlated features from the following code:

corrmat = X_train_unique.corr()

def get_correlation(data, threshold):
    corr_col = set()
    corrmat = data.corr()
    for i in range(len(corrmat.columns)):
        for j in range(i):
            if abs(corrmat.iloc[i, j]) > threshold:
                colname = corrmat.columns[i]
                corr_col.add(colname)
    return corr_col

corr_features = get_correlation(X_train_unique, 0.70)
print('correlated features: ', len(set(corr_features)) )

correlated features:  148

X_train_uncorr = X_train_unique.drop(labels=corr_features, axis = 1)
X_test_uncorr = X_test_unique.drop(labels = corr_features, axis = 1)
X_train_uncorr.shape, X_test_uncorr.shape

((16000, 79), (4000, 79))

Here, we can observe that the features are reduced from 371 to 79 features.

Feature Dimention Reduction by LDA or Is it a Classifier

Here the question is, is it dimentional reduction technique or is it a classifier. But we can say it is working for both.

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

The number of components which we can pass here is 1 why beacuse if you remember the maximum number of components we can select are total number of classes - 1. Here, santadard problem is a biclass problem those are either 0 or 1. so the maximum number of components is 1.
Even if we select more than 1, it will treat as 1.

Let's go ahead and transform the data by using fit_transform().

lda = LDA(n_components=1)
X_train_lda = lda.fit_transform(X_train_uncorr, y_train)
X_test_lda = lda.transform(X_test_uncorr)

Here, we can see transformed data from the following code.

X_train_lda.shape, X_test_lda.shape

((16000, 1), (4000, 1))

def run_randomForest(X_train, X_test, y_train, y_test):
    clf = RandomForestClassifier(n_estimators=100, random_state=0, n_jobs=-1)
    clf.fit(X_train, y_train)
    y_pred = clf.predict(X_test)
    print('Accuracy on test set: ')
    print(accuracy_score(y_test, y_pred))

%%time
run_randomForest(X_train_lda, X_test_lda, y_train, y_test)

Accuracy on test set: 
0.93025
CPU times: user 3.35 s, sys: 64.3 ms, total: 3.41 s
Wall time: 1.1 s

%%time
run_randomForest(X_train_uncorr, X_test_uncorr, y_train, y_test)

Accuracy on test set: 
0.9585
CPU times: user 3.41 s, sys: 82 ms, total: 3.49 s
Wall time: 1.2 s

Let's go ahead and run this on the original dataset.

%%time
run_randomForest(X_train, X_test, y_train, y_test)

Accuracy on test set: 
0.9585
CPU times: user 6.68 s, sys: 143 ms, total: 6.83 s
Wall time: 2.01 s

So, if see here accuracy on the original dataset is more compared to transformed dataset. But, the training time original dataset is double than tranformed version and the dimension also has been reduced.

From this, we can observe LDA won't give guarantee on the accuracy but it will give guarantee on the reduction in dimension and cpu time.

Feature Reduction by PCA

from sklearn.decomposition import PCA

Let's remove the features by using the Principal Component Analysis (PCA) method.

pca = PCA(n_components=2, random_state=42)
pca.fit(X_train_uncorr)
PCA(copy=True, iterated_power='auto', n_components=2, random_state=42, svd_solver='auto', tol=0.0, whiten=False)

Let's go ahead and get training and testing dataset by PCA transformation.

X_train_pca = pca.transform(X_train_uncorr)
X_test_pca = pca.transform(X_test_uncorr)
X_train_pca.shape, X_test_pca.shape

((16000, 2), (4000, 2))

Now, find out the accuracy and cpu time of the transformed dataset.

%%time
run_randomForest(X_train_pca, X_test_pca, y_train, y_test)

Accuracy on test set: 
0.956
CPU times: user 3.06 s, sys: 67.9 ms, total: 3.12 s
Wall time: 999 ms

Let's get the accuracy and cpu time of the original dataset.

%%time
run_randomForest(X_train, X_test, y_train, y_test)

Accuracy on test set: 
0.9585
CPU times: user 6.75 s, sys: 138 ms, total: 6.89 s
Wall time: 2.13 s

Let's check the dimension of the uncorrected dataset.

X_train_uncorr.shape

(16000, 79)

Let's check the accuracy for various selected components.

for component in range(1,5):
    pca = PCA(n_components=component, random_state=42)
    pca.fit(X_train_uncorr)
    X_train_pca = pca.transform(X_train_uncorr)
    X_test_pca = pca.transform(X_test_uncorr)
    print('Selected Components: ', component)
    run_randomForest(X_train_pca, X_test_pca, y_train, y_test)
    print()

Selected Components:  1
Accuracy on test set: 
0.92375

Selected Components:  2
Accuracy on test set: 
0.956

Selected Components:  3
Accuracy on test set: 
0.95675

Selected Components:  4
Accuracy on test set: 
0.95825