Feature Selection with Filtering Method | Constant, Quasi Constant and Duplicate Feature Removal
Filtering method
Watch Full Playlist: https://www.youtube.com/playlist?list=PLc2rvfiptPSQYzmDIFuq2PqN2n28ZjxDH
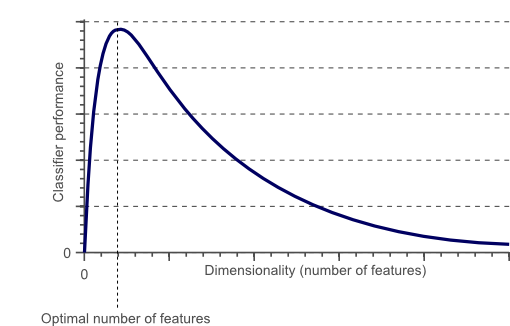
Unnecessary and redundant features not only slow down the training time of an algorithm, but they also affect the performance of the algorithm.
There are several advantages of performing feature selection before training machine learning models:
- Models with less number of features have higher explainability.
- It is easier to implement machine learning models with reduced features.
- Fewer features lead to enhanced generalization which in turn reduces overfitting.
- Feature selection removes data redundancy.
- Training time of models with fewer features is significantly lower.
- Models with fewer features are less prone to errors.
What is filter method?
Features selected using filter methods can be used as an input to any machine learning models.
- Univariate -> Fisher Score, Mutual Information Gain, Variance etc
- Multi-variate -> Pearson Correlation
The univariate filter methods are the type of methods where individual features are ranked according to specific criteria. The top N features are then selected. Different types of ranking criteria are used for univariate filtermethods, for example fisher score, mutual information, and variance of the feature.
Multivariate filter methods are capable of removing redundant features from the data since they take the mutual relationship between the features into account.
Univariate Filtering Methods in this lesson
- Constant Removal
- Quasi Constant Removal
- Duplicate Feature Removal
Download Data Files
Constant Feature Removal
Importing required libraries
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns
from sklearn.model_selection import train_test_split from sklearn.ensemble import RandomForestClassifier from sklearn.metrics import accuracy_score from sklearn.feature_selection import VarianceThreshold
Now read the dataset from pandas and intially number of rows are 20000.
data = pd.read_csv('santander.csv', nrows = 20000)
data.head()
| ID | var3 | var15 | imp_ent_var16_ult1 | imp_op_var39_comer_ult1 | imp_op_var39_comer_ult3 | imp_op_var40_comer_ult1 | imp_op_var40_comer_ult3 | imp_op_var40_efect_ult1 | imp_op_var40_efect_ult3 | ... | saldo_medio_var33_hace2 | saldo_medio_var33_hace3 | saldo_medio_var33_ult1 | saldo_medio_var33_ult3 | saldo_medio_var44_hace2 | saldo_medio_var44_hace3 | saldo_medio_var44_ult1 | saldo_medio_var44_ult3 | var38 | TARGET | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 23 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0 | 0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 39205.170000 | 0 |
| 1 | 3 | 2 | 34 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0 | 0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 49278.030000 | 0 |
| 2 | 4 | 2 | 23 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0 | 0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 67333.770000 | 0 |
| 3 | 8 | 2 | 37 | 0.0 | 195.0 | 195.0 | 0.0 | 0.0 | 0 | 0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 64007.970000 | 0 |
| 4 | 10 | 2 | 39 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0 | 0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 117310.979016 | 0 |
5 rows × 371 columns
Let's load these datasets into x and y vectors.
X = data.drop('TARGET', axis = 1)
y = data['TARGET']
X.shape, y.shape
((20000, 370), (20000,))
Let's split this dataset into train and test datasets using the below code.
Here test_size = 0.2 that means 20% for testing and remaining for training the model.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0, stratify = y)
Constant Features Removal
In this, first we need to create a variance threshold and then fit the model with training set of the data.
constant_filter = VarianceThreshold(threshold=0) constant_filter.fit(X_train)
VarianceThreshold(threshold=0)
Let's get the number of features left after removing constant features.
constant_filter.get_support().sum()
291
Let's print the constant features list.
constant_list = [not temp for temp in constant_filter.get_support()] constant_list
[False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, True, True, False, False, False, False, False, False, False, False, False, False, False, False, False, True, True, False, False, False, False, False, True, True, False, False, False, False, False, False, False, False, False, False, False, True, True, True, True, False, False, False, False, False, False, False, False, False, False, False, True, True, False, False, False, False, False, False, False, True, False, False, False, True, True, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, True, True, False, False, False, False, False, True, True, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, True, True, True, True, False, False, False, False, False, False, False, False, False, False, True, True, False, False, False, False, False, False, False, False, True, False, False, False, False, False, True, True, False, False, False, False, False, False, False, True, False, False, False, True, False, False, False, False, True, True, False, False, False, False, False, True, False, False, True, False, False, True, False, True, True, False, False, False, False, False, False, True, False, True, False, True, False, False, False, False, False, False, False, True, False, True, False, True, False, True, True, True, True, False, False, False, False, False, False, True, False, False, False, True, False, True, False, True, True, False, False, True, False, True, True, True, False, True, True, False, False, True, False, False, False, False, False, False, False, False, True, True, False, False, False, False, False, False, True, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, True, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, True, False, True, False, True, True, False, False, False, False, True, False, True, True, True, False, True, True, False, False, False, False, False, False, True, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, True, True, True, True, False, False, False, False, False, True, False, False, False, False, False, False, False, False, False, False, False]
Now we will try get the name of features which are constant.
X.columns[constant_list]
Index(['ind_var2_0', 'ind_var2', 'ind_var13_medio_0', 'ind_var13_medio',
'ind_var18_0', 'ind_var18', 'ind_var27_0', 'ind_var28_0', 'ind_var28',
'ind_var27', 'ind_var34_0', 'ind_var34', 'ind_var41', 'ind_var46_0',
'ind_var46', 'num_var13_medio_0', 'num_var13_medio', 'num_var18_0',
'num_var18', 'num_var27_0', 'num_var28_0', 'num_var28', 'num_var27',
'num_var34_0', 'num_var34', 'num_var41', 'num_var46_0', 'num_var46',
'saldo_var13_medio', 'saldo_var18', 'saldo_var28', 'saldo_var27',
'saldo_var34', 'saldo_var41', 'saldo_var46',
'delta_imp_amort_var18_1y3', 'delta_imp_amort_var34_1y3',
'delta_imp_reemb_var33_1y3', 'delta_imp_trasp_var17_out_1y3',
'delta_imp_trasp_var33_out_1y3', 'delta_num_reemb_var33_1y3',
'delta_num_trasp_var17_out_1y3', 'delta_num_trasp_var33_out_1y3',
'imp_amort_var18_hace3', 'imp_amort_var18_ult1',
'imp_amort_var34_hace3', 'imp_amort_var34_ult1', 'imp_var7_emit_ult1',
'imp_reemb_var13_hace3', 'imp_reemb_var17_hace3',
'imp_reemb_var33_hace3', 'imp_reemb_var33_ult1',
'imp_trasp_var17_in_hace3', 'imp_trasp_var17_out_hace3',
'imp_trasp_var17_out_ult1', 'imp_trasp_var33_in_hace3',
'imp_trasp_var33_out_hace3', 'imp_trasp_var33_out_ult1',
'ind_var7_emit_ult1', 'num_var2_0_ult1', 'num_var2_ult1',
'num_var7_emit_ult1', 'num_meses_var13_medio_ult3',
'num_reemb_var13_hace3', 'num_reemb_var17_hace3',
'num_reemb_var33_hace3', 'num_reemb_var33_ult1',
'num_trasp_var17_in_hace3', 'num_trasp_var17_out_hace3',
'num_trasp_var17_out_ult1', 'num_trasp_var33_in_hace3',
'num_trasp_var33_out_hace3', 'num_trasp_var33_out_ult1',
'saldo_var2_ult1', 'saldo_medio_var13_medio_hace2',
'saldo_medio_var13_medio_hace3', 'saldo_medio_var13_medio_ult1',
'saldo_medio_var13_medio_ult3', 'saldo_medio_var29_hace3'],
dtype='object')
Let's go ahead and transform the x_train and x_test datasets into non constant datasets.
X_train_filter = constant_filter.transform(X_train) X_test_filter = constant_filter.transform(X_test)
Let's get the shape of the datasets.
X_train_filter.shape, X_test_filter.shape, X_train.shape
((16000, 291), (4000, 291), (16000, 370))
Quasi constant feature removal
These are the filters that are almost constant or quasi constant in other words these features have same values for large subset of outputs and such features are not very useful for making predictions.
There is no rule for fixing threshold value but generally we can take as 99% similarity and 1% of non similarity.
Let's go ahead see how many quasi constant features are there.
quasi_constant_filter = VarianceThreshold(threshold=0.01) quasi_constant_filter.fit(X_train_filter) VarianceThreshold(threshold=0.01)
Let's see how many features are non quasi constant.
quasi_constant_filter.get_support().sum()
245
291-245
46
To remove those quasi constant features, we need to apply transform on quasi transform filter object.
X_train_quasi_filter = quasi_constant_filter.transform(X_train_filter) X_test_quasi_filter = quasi_constant_filter.transform(X_test_filter) X_train_quasi_filter.shape, X_test_quasi_filter.shape
((16000, 245), (4000, 245))
370-245
125
In this way, we have reduced features from 370 to 245 features.
Remove Duplicate Features
If two features are exactly same those are called as duplicate features that means these features doesn't provide any new information and makes our model complex.
Here we have a problem as we did in quasi constant and constant removal sklearn doesn't have direct library to handle with duplicate features .
So, first we will do transpose the dataset and then python have a method to remove duplicate features.
Let's transpose the training and testing dataset by using following code.
X_train_T = X_train_quasi_filter.T X_test_T = X_test_quasi_filter.T type(X_train_T) numpy.ndarray
Let's change into pandas dataframe.
X_train_T = pd.DataFrame(X_train_T) X_test_T = pd.DataFrame(X_test_T)
Let's check the shapes of the datasets.
X_train_T.shape, X_test_T.shape
((245, 16000), (245, 4000))
Let's go ahead and get the duplicate features.
X_train_T.duplicated().sum()
18
So, here we have 18 duplicated features.
duplicated_features = X_train_T.duplicated() duplicated_features
0 False
1 False
2 False
3 False
4 False
5 False
6 False
7 False
8 False
9 False
10 False
11 False
12 False
13 False
14 False
15 False
16 False
17 False
18 False
19 False
20 False
21 False
22 False
23 False
24 False
25 False
26 False
27 False
28 False
29 False
...
215 False
216 False
217 False
218 False
219 False
220 False
221 False
222 False
223 False
224 False
225 False
226 False
227 False
228 False
229 False
230 False
231 False
232 False
233 False
234 False
235 False
236 False
237 False
238 False
239 False
240 False
241 False
242 False
243 False
244 False
Length: 245, dtype: bool
Now, we need to get to non duplicated features from the following code.
features_to_keep = [not index for index in duplicated_features]
Let's do transpose again to get the original shape.
X_train_unique = X_train_T[features_to_keep].T X_test_unique = X_test_T[features_to_keep].T
Let's check the shape of the datasets.
X_train_unique.shape, X_train.shape
((16000, 227), (16000, 370))
Here, we can observe original dataset has 370 features and after removal of quasi constant, constant and duplicate features we have 227 features.
370-227
143
Build ML model and compare the performance of the selected feature
Let's go ahead and compare the model between original dataset and transformed dataset.
Here we are going to build random forest classifier.
def run_randomForest(X_train, X_test, y_train, y_test):
clf = RandomForestClassifier(n_estimators=100, random_state=0, n_jobs=-1)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('Accuracy on test set: ')
print(accuracy_score(y_test, y_pred))
Let's calculate the accuracy.
%%time run_randomForest(X_train_unique, X_test_unique, y_train, y_test)
Accuracy on test set: 0.95875 Wall time: 2.18 s
Let's check the accuracy of the original dataset.
%%time run_randomForest(X_train, X_test, y_train, y_test)
Accuracy on test set: 0.9585 Wall time: 2.87 s
(1.51-1.26)*100/1.51
16.556291390728475
Feature Selection with Filtering Method- Correlated Feature Removal
A dataset can also contain correlated features. Two or more than two features are correlated if they are close to each other in the linear space.
Correlation between the output observations and the input features is very important and such features should be retained.

Summary
- Feature Space to target correlation is desired
- Feature to feature correlation is not desired
- If 2 features are highly correlated then either feature is redundant
- Correlation in feature space increases model complexity
- Removing correlated features improves model performance
- Different model shows different performance over the correlated features
corrmat = X_train_unique.corr() plt.figure(figsize=(12,8)) sns.heatmap(corrmat)

def get_correlation(data, threshold):
corr_col = set()
corrmat = data.corr()
for i in range(len(corrmat.columns)):
for j in range(i):
if abs(corrmat.iloc[i, j])> threshold:
colname = corrmat.columns[i]
corr_col.add(colname)
return corr_col
corr_features = get_correlation(X_train_unique, 0.85) corr_features
{5,
7,
9,
11,
12,
14,
15,
16,
17,
18,
23,
24,
28,
29,
30,
32,
33,
35,
36,
38,
42,
46,
47,
50,
51,
52,
53,
54,
55,
56,
57,
58,
60,
61,
62,
65,
67,
68,
69,
70,
72,
76,
80,
81,
82,
83,
84,
86,
87,
88,
91,
93,
95,
98,
100,
101,
103,
104,
111,
115,
117,
120,
121,
125,
136,
138,
143,
146,
149,
153,
154,
157,
158,
161,
162,
163,
164,
169,
170,
173,
180,
182,
183,
184,
185,
188,
189,
190,
191,
192,
193,
194,
195,
197,
198,
199,
204,
205,
207,
208,
215,
216,
217,
219,
220,
221,
223,
224,
227,
228,
229,
230,
231,
232,
234,
235,
236,
237,
238,
239,
240,
241,
242,
243}
Let's get the length of the correlated features.
len(corr_features)
124
Let's drop the correlated features from the dataset.
X_train_uncorr = X_train_unique.drop(labels=corr_features, axis = 1) X_test_uncorr = X_test_unique.drop(labels = corr_features, axis = 1) X_train_uncorr.shape, X_test_uncorr.shape
((16000, 103), (4000, 103))
Let's find out the accuracy and training time of the uncorrelated dataset.
%%time run_randomForest(X_train_uncorr, X_test_uncorr, y_train, y_test)
Accuracy on test set: 0.95875 Wall time: 912 ms
Now we will find out the accuracy and training time of the original daatset.
%%time run_randomForest(X_train, X_test, y_train, y_test)
Accuracy on test set: 0.9585 Wall time: 1.53 s
(1.53-0.912)*100/1.53
40.3921568627451
Feature Grouping and Feature Importance
corrmat
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.000000 | -0.025277 | -0.001942 | 0.003594 | 0.004054 | -0.001697 | -0.015882 | -0.019807 | 0.000956 | -0.000588 | ... | -0.001337 | 0.002051 | -0.008500 | 0.006554 | 0.005907 | 0.008825 | -0.009174 | 0.012031 | 0.012128 | 0.006612 |
| 1 | -0.025277 | 1.000000 | -0.007647 | 0.001819 | 0.008981 | 0.009232 | 0.001638 | 0.001746 | 0.000614 | 0.000695 | ... | 0.000544 | 0.000586 | 0.000337 | 0.000550 | 0.000563 | 0.000922 | 0.000598 | 0.000875 | 0.000942 | 0.000415 |
| 2 | -0.001942 | -0.007647 | 1.000000 | 0.030919 | 0.106245 | 0.109140 | 0.048524 | 0.055708 | 0.004040 | 0.005796 | ... | 0.025522 | 0.020168 | 0.011550 | 0.019325 | 0.019527 | 0.041321 | 0.016172 | 0.043577 | 0.044281 | -0.000810 |
| 3 | 0.003594 | 0.001819 | 0.030919 | 1.000000 | 0.029418 | 0.024905 | 0.014513 | 0.013857 | -0.000613 | -0.000691 | ... | 0.014032 | -0.000583 | -0.000337 | -0.000548 | -0.000561 | 0.000541 | -0.000577 | 0.000231 | 0.000235 | 0.000966 |
| 4 | 0.004054 | 0.008981 | 0.106245 | 0.029418 | 1.000000 | 0.888789 | 0.381632 | 0.341266 | 0.012927 | 0.019674 | ... | 0.002328 | 0.016743 | -0.001662 | 0.020509 | 0.021276 | -0.001905 | -0.000635 | -0.002552 | -0.002736 | 0.003656 |
| 5 | -0.001697 | 0.009232 | 0.109140 | 0.024905 | 0.888789 | 1.000000 | 0.363680 | 0.384820 | 0.017671 | 0.030060 | ... | 0.000328 | 0.010860 | -0.001706 | 0.012963 | 0.013553 | 0.000871 | 0.007096 | -0.001672 | -0.001844 | 0.002257 |
| 6 | -0.015882 | 0.001638 | 0.048524 | 0.014513 | 0.381632 | 0.363680 | 1.000000 | 0.908158 | 0.030397 | 0.036359 | ... | -0.000485 | 0.006351 | -0.000301 | 0.002590 | 0.003867 | -0.000818 | -0.000515 | -0.000779 | -0.000839 | 0.004448 |
| 7 | -0.019807 | 0.001746 | 0.055708 | 0.013857 | 0.341266 | 0.384820 | 0.908158 | 1.000000 | 0.047667 | 0.056456 | ... | -0.000514 | 0.006336 | -0.000318 | 0.002476 | 0.003707 | -0.000866 | -0.000545 | -0.000825 | -0.000888 | 0.002427 |
| 8 | 0.000956 | 0.000614 | 0.004040 | -0.000613 | 0.012927 | 0.017671 | 0.030397 | 0.047667 | 1.000000 | 0.988256 | ... | -0.000184 | -0.000197 | -0.000114 | -0.000185 | -0.000189 | -0.000309 | -0.000195 | -0.000295 | -0.000317 | -0.000739 |
| 9 | -0.000588 | 0.000695 | 0.005796 | -0.000691 | 0.019674 | 0.030060 | 0.036359 | 0.056456 | 0.988256 | 1.000000 | ... | -0.000207 | -0.000222 | -0.000128 | -0.000208 | -0.000213 | -0.000349 | -0.000220 | -0.000332 | -0.000358 | -0.000811 |
| 10 | -0.012443 | 0.001517 | 0.042368 | 0.012451 | 0.298916 | 0.280081 | 0.805265 | 0.706608 | 0.388309 | 0.398826 | ... | -0.000452 | -0.000485 | -0.000280 | -0.000213 | -0.000100 | -0.000762 | -0.000480 | -0.000726 | -0.000782 | 0.003341 |
| 11 | 0.010319 | 0.009097 | 0.096719 | 0.026377 | 0.938409 | 0.824893 | 0.038751 | 0.029445 | 0.002612 | 0.007677 | ... | 0.002699 | 0.015727 | -0.001684 | 0.021203 | 0.021555 | -0.001754 | -0.000494 | -0.002467 | -0.002645 | 0.002290 |
| 12 | 0.005268 | 0.009360 | 0.098070 | 0.021968 | 0.838953 | 0.943622 | 0.067664 | 0.057591 | 0.002018 | 0.012266 | ... | 0.000540 | 0.009474 | -0.001732 | 0.013133 | 0.013330 | 0.001253 | 0.007871 | -0.001513 | -0.001676 | 0.001570 |
| 13 | 0.017605 | -0.002511 | 0.082025 | 0.016331 | 0.266746 | 0.254702 | 0.040788 | 0.033996 | 0.108329 | 0.106806 | ... | -0.001670 | 0.034002 | -0.001035 | 0.038103 | 0.038047 | 0.007400 | 0.002248 | 0.006688 | 0.006283 | 0.000707 |
| 14 | 0.016960 | -0.001086 | 0.095485 | 0.016458 | 0.326051 | 0.359897 | 0.048914 | 0.045136 | 0.081030 | 0.081962 | ... | -0.002040 | 0.025566 | -0.001264 | 0.028641 | 0.028613 | 0.004485 | 0.001176 | 0.004012 | 0.003599 | -0.001992 |
| 15 | 0.018040 | 0.002426 | 0.106415 | 0.024014 | 0.638412 | 0.565620 | 0.043920 | 0.033716 | 0.083438 | 0.084688 | ... | 0.000009 | 0.033265 | -0.001589 | 0.038978 | 0.039103 | 0.004773 | 0.001465 | 0.003984 | 0.003632 | 0.001339 |
| 16 | 0.017400 | -0.002401 | 0.081028 | 0.015979 | 0.263482 | 0.252160 | 0.043357 | 0.038548 | 0.214397 | 0.211633 | ... | -0.001661 | 0.033386 | -0.001029 | 0.037417 | 0.037362 | 0.007237 | 0.002188 | 0.006539 | 0.006139 | 0.000614 |
| 17 | 0.016745 | -0.001019 | 0.095009 | 0.016239 | 0.324417 | 0.358769 | 0.051373 | 0.049260 | 0.160240 | 0.162113 | ... | -0.002037 | 0.025295 | -0.001262 | 0.028341 | 0.028312 | 0.004412 | 0.001147 | 0.003946 | 0.003534 | -0.002038 |
| 18 | 0.015206 | 0.002629 | 0.110912 | 0.025558 | 0.673593 | 0.599584 | 0.190138 | 0.162168 | 0.152035 | 0.155173 | ... | -0.000074 | 0.032155 | -0.001591 | 0.037742 | 0.037884 | 0.004487 | 0.001333 | 0.003729 | 0.003377 | 0.001910 |
| 19 | -0.000103 | 0.000519 | 0.016886 | -0.000520 | 0.049579 | 0.042621 | 0.012454 | 0.007797 | -0.000175 | -0.000198 | ... | -0.000156 | -0.000167 | -0.000096 | -0.000156 | -0.000160 | -0.000262 | -0.000165 | -0.000250 | -0.000269 | 0.000213 |
| 20 | -0.001198 | 0.004590 | 0.107680 | 0.007478 | 0.227803 | 0.238159 | 0.306165 | 0.284353 | 0.125108 | 0.138077 | ... | -0.001365 | -0.001462 | -0.000846 | 0.000768 | 0.001829 | 0.009008 | -0.001449 | 0.009156 | 0.011164 | -0.001227 |
| 21 | -0.006814 | -0.008975 | -0.105502 | -0.002101 | -0.208030 | -0.211873 | -0.071459 | -0.078593 | -0.012763 | -0.021318 | ... | 0.002674 | -0.049920 | -0.037729 | -0.038529 | -0.041438 | -0.000421 | -0.010257 | 0.002149 | 0.002306 | -0.016447 |
| 22 | -0.002037 | 0.041015 | -0.102487 | 0.017541 | 0.041167 | 0.041372 | -0.006549 | -0.008179 | 0.003576 | 0.001088 | ... | 0.009114 | -0.012641 | -0.011070 | -0.008324 | -0.009368 | 0.013263 | 0.004114 | 0.013717 | 0.014768 | -0.056029 |
| 23 | 0.010356 | 0.008019 | 0.107570 | 0.003429 | 0.200514 | 0.182937 | 0.035401 | 0.025512 | 0.012907 | 0.018006 | ... | -0.002401 | 0.031418 | -0.001487 | 0.033291 | 0.034573 | 0.001397 | 0.011918 | -0.001487 | -0.001591 | 0.012346 |
| 24 | 0.012021 | 0.007439 | 0.101605 | 0.004843 | 0.220673 | 0.201909 | 0.039018 | 0.028469 | 0.014240 | 0.019760 | ... | -0.002227 | 0.034079 | -0.001380 | 0.036066 | 0.037450 | 0.002086 | 0.013156 | -0.001036 | -0.001105 | -0.003767 |
| 25 | 0.001732 | 0.011525 | 0.273152 | 0.010099 | 0.027387 | 0.026378 | 0.046258 | 0.033114 | -0.003889 | -0.004384 | ... | -0.003450 | 0.020817 | -0.002138 | 0.022279 | 0.023163 | -0.000543 | -0.003662 | -0.001555 | -0.001463 | 0.012034 |
| 26 | 0.001138 | 0.009467 | 0.231649 | 0.015117 | 0.033757 | 0.037053 | 0.044225 | 0.034049 | -0.003194 | -0.003600 | ... | -0.002834 | 0.026148 | -0.001756 | 0.027806 | 0.028888 | 0.001500 | -0.003008 | 0.000193 | 0.000460 | 0.006643 |
| 27 | -0.004836 | 0.009771 | 0.299165 | 0.036569 | -0.010411 | -0.013701 | 0.020327 | 0.019508 | -0.003295 | -0.003715 | ... | -0.002924 | -0.003132 | -0.001811 | -0.001902 | -0.001440 | -0.003893 | -0.003103 | -0.003587 | -0.003989 | 0.012240 |
| 28 | -0.006480 | 0.008796 | 0.241707 | 0.040420 | -0.012628 | -0.018755 | 0.009992 | 0.003331 | -0.002969 | -0.003347 | ... | -0.002634 | -0.002822 | -0.001632 | -0.001507 | -0.000986 | -0.004438 | -0.002796 | -0.004228 | -0.004553 | 0.007400 |
| 29 | -0.005811 | 0.008676 | 0.237830 | 0.041165 | -0.012035 | -0.018146 | 0.010326 | 0.003592 | -0.002929 | -0.003301 | ... | -0.002599 | -0.002784 | -0.001610 | -0.001456 | -0.000927 | -0.004378 | -0.002758 | -0.004171 | -0.004491 | 0.006121 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 215 | 0.006937 | 0.002152 | 0.043278 | 0.002314 | 0.073627 | 0.084908 | 0.009789 | 0.009653 | 0.000540 | 0.013546 | ... | -0.000644 | 0.003153 | -0.000399 | 0.003511 | 0.003709 | 0.082936 | 0.230452 | 0.029915 | 0.033617 | 0.000338 |
| 216 | 0.004924 | 0.002210 | 0.045622 | 0.003234 | 0.086904 | 0.093401 | 0.042081 | 0.029906 | 0.000420 | 0.012702 | ... | -0.000662 | 0.003721 | -0.000410 | 0.004129 | 0.004359 | 0.074334 | 0.206808 | 0.026758 | 0.030066 | 0.000244 |
| 217 | 0.008100 | 0.003979 | 0.149586 | 0.001554 | -0.003401 | -0.004867 | 0.024589 | 0.017603 | -0.001336 | -0.001506 | ... | -0.001185 | 0.011108 | -0.000734 | 0.011385 | 0.011627 | -0.001886 | -0.001258 | -0.001828 | -0.001966 | 0.017276 |
| 218 | -0.000582 | 0.002581 | 0.093124 | -0.001262 | -0.007050 | -0.006547 | -0.002282 | -0.002111 | -0.000865 | -0.000976 | ... | -0.000768 | 0.012837 | -0.000476 | 0.013076 | 0.013340 | -0.001294 | -0.000815 | -0.001232 | -0.001327 | 0.006644 |
| 219 | 0.007130 | 0.004811 | 0.178546 | 0.002540 | -0.002079 | -0.004782 | 0.036168 | 0.025934 | -0.001618 | -0.001823 | ... | -0.001435 | 0.010157 | -0.000889 | 0.010430 | 0.010646 | -0.002222 | -0.001523 | -0.002103 | -0.002237 | 0.018092 |
| 220 | 0.007675 | 0.004879 | 0.179565 | 0.002948 | -0.001151 | -0.003808 | 0.038964 | 0.028107 | -0.001640 | -0.001849 | ... | -0.001455 | 0.009732 | -0.000902 | 0.010011 | 0.010224 | -0.002257 | -0.001545 | -0.002116 | -0.002243 | 0.017579 |
| 221 | -0.006477 | 0.005759 | 0.178263 | -0.005438 | 0.002963 | -0.001631 | 0.048470 | 0.029154 | -0.001943 | -0.002190 | ... | -0.001724 | -0.001846 | -0.001068 | -0.001729 | -0.001768 | -0.002904 | -0.001829 | -0.002766 | -0.002979 | 0.014736 |
| 222 | -0.010219 | 0.003183 | 0.094741 | -0.003083 | 0.040691 | 0.027749 | 0.133603 | 0.084716 | -0.001073 | -0.001210 | ... | -0.000952 | -0.001020 | -0.000590 | -0.000958 | -0.000981 | -0.001604 | -0.001011 | -0.001528 | -0.001646 | 0.002052 |
| 223 | -0.011386 | 0.006355 | 0.200415 | 0.025778 | -0.000914 | -0.005809 | 0.038767 | 0.022672 | -0.002144 | -0.002417 | ... | -0.001903 | -0.002038 | -0.001179 | -0.001788 | -0.001769 | -0.003205 | -0.002019 | -0.003054 | -0.003288 | 0.014980 |
| 224 | -0.011200 | 0.006248 | 0.195652 | 0.033042 | -0.000322 | -0.005729 | 0.043137 | 0.025504 | -0.002108 | -0.002376 | ... | -0.001871 | -0.002004 | -0.001159 | -0.001801 | -0.001804 | -0.003151 | -0.001985 | -0.003002 | -0.003233 | 0.014628 |
| 225 | 0.006455 | 0.002629 | 0.125618 | -0.001532 | 0.003267 | 0.004018 | 0.013532 | 0.021485 | -0.000883 | -0.000995 | ... | -0.000783 | -0.000839 | -0.000485 | -0.000788 | -0.000807 | -0.001195 | -0.000831 | -0.001146 | -0.001241 | 0.014567 |
| 226 | 0.008361 | 0.001482 | 0.059293 | 0.000238 | 0.012429 | 0.010896 | 0.001034 | 0.002878 | -0.000492 | -0.000555 | ... | -0.000437 | -0.000468 | -0.000271 | -0.000439 | -0.000450 | -0.000573 | -0.000463 | -0.000556 | -0.000608 | 0.005688 |
| 227 | 0.003765 | 0.002827 | 0.135362 | -0.001817 | 0.000824 | 0.001493 | 0.012108 | 0.019415 | -0.000950 | -0.001071 | ... | -0.000843 | -0.000903 | -0.000522 | -0.000848 | -0.000868 | -0.001417 | -0.000895 | -0.001348 | -0.001452 | 0.015351 |
| 228 | 0.005352 | 0.002770 | 0.132537 | -0.001698 | 0.001272 | 0.001627 | 0.010082 | 0.016429 | -0.000930 | -0.001048 | ... | -0.000825 | -0.000884 | -0.000511 | -0.000830 | -0.000850 | -0.001387 | -0.000876 | -0.001318 | -0.001421 | 0.014485 |
| 229 | 0.008042 | 0.000356 | 0.023435 | -0.000354 | -0.001629 | -0.001719 | -0.000318 | -0.000337 | -0.000120 | -0.000136 | ... | -0.000107 | 0.002856 | -0.000066 | 0.004306 | 0.004022 | 0.000265 | -0.000113 | 0.000089 | 0.000121 | 0.013197 |
| 230 | 0.007870 | 0.000338 | 0.022679 | -0.000338 | -0.001669 | -0.001713 | -0.000302 | -0.000320 | -0.000114 | -0.000129 | ... | -0.000101 | -0.000108 | -0.000063 | -0.000102 | -0.000104 | -0.000171 | -0.000107 | -0.000163 | -0.000175 | 0.012842 |
| 231 | 0.007952 | 0.000411 | 0.025362 | -0.000285 | -0.001677 | -0.001846 | -0.000365 | -0.000387 | -0.000138 | -0.000156 | ... | -0.000123 | 0.007701 | -0.000076 | 0.011513 | 0.010768 | 0.001004 | -0.000130 | 0.000510 | 0.000619 | 0.013321 |
| 232 | 0.008021 | 0.000408 | 0.025406 | -0.000334 | -0.001730 | -0.001875 | -0.000362 | -0.000383 | -0.000137 | -0.000154 | ... | -0.000121 | 0.006078 | -0.000075 | 0.009101 | 0.008510 | 0.000746 | -0.000129 | 0.000360 | 0.000443 | 0.013418 |
| 233 | -0.001596 | 0.000391 | 0.013612 | -0.000391 | -0.001930 | -0.001981 | -0.000349 | -0.000370 | -0.000132 | -0.000149 | ... | 0.538270 | -0.000125 | -0.000073 | -0.000118 | -0.000121 | 0.031970 | -0.000124 | 0.068648 | 0.057673 | -0.000203 |
| 234 | 0.001830 | 0.000453 | 0.023446 | 0.008469 | 0.000833 | -0.000407 | -0.000404 | -0.000428 | -0.000153 | -0.000172 | ... | 0.950232 | -0.000145 | -0.000084 | -0.000136 | -0.000140 | 0.004649 | -0.000144 | 0.010219 | 0.008541 | -0.003446 |
| 235 | -0.001337 | 0.000544 | 0.025522 | 0.014032 | 0.002328 | 0.000328 | -0.000485 | -0.000514 | -0.000184 | -0.000207 | ... | 1.000000 | -0.000174 | -0.000101 | -0.000164 | -0.000168 | 0.012705 | -0.000173 | 0.027515 | 0.023072 | -0.003399 |
| 236 | 0.002051 | 0.000586 | 0.020168 | -0.000583 | 0.016743 | 0.010860 | 0.006351 | 0.006336 | -0.000197 | -0.000222 | ... | -0.000174 | 1.000000 | 0.484331 | 0.938668 | 0.953411 | 0.021540 | -0.000185 | 0.012393 | 0.014523 | -0.000773 |
| 237 | -0.008500 | 0.000337 | 0.011550 | -0.000337 | -0.001662 | -0.001706 | -0.000301 | -0.000318 | -0.000114 | -0.000128 | ... | -0.000101 | 0.484331 | 1.000000 | 0.193281 | 0.225912 | -0.000170 | -0.000107 | -0.000162 | -0.000174 | -0.000402 |
| 238 | 0.006554 | 0.000550 | 0.019325 | -0.000548 | 0.020509 | 0.012963 | 0.002590 | 0.002476 | -0.000185 | -0.000208 | ... | -0.000164 | 0.938668 | 0.193281 | 1.000000 | 0.998497 | 0.032162 | -0.000174 | 0.018565 | 0.021742 | -0.000525 |
| 239 | 0.005907 | 0.000563 | 0.019527 | -0.000561 | 0.021276 | 0.013553 | 0.003867 | 0.003707 | -0.000189 | -0.000213 | ... | -0.000168 | 0.953411 | 0.225912 | 0.998497 | 1.000000 | 0.030087 | -0.000178 | 0.017358 | 0.020331 | -0.000589 |
| 240 | 0.008825 | 0.000922 | 0.041321 | 0.000541 | -0.001905 | 0.000871 | -0.000818 | -0.000866 | -0.000309 | -0.000349 | ... | 0.012705 | 0.021540 | -0.000170 | 0.032162 | 0.030087 | 1.000000 | 0.329805 | 0.935317 | 0.919036 | 0.011106 |
| 241 | -0.009174 | 0.000598 | 0.016172 | -0.000577 | -0.000635 | 0.007096 | -0.000515 | -0.000545 | -0.000195 | -0.000220 | ... | -0.000173 | -0.000185 | -0.000107 | -0.000174 | -0.000178 | 0.329805 | 1.000000 | 0.127224 | 0.140902 | 0.011807 |
| 242 | 0.012031 | 0.000875 | 0.043577 | 0.000231 | -0.002552 | -0.001672 | -0.000779 | -0.000825 | -0.000295 | -0.000332 | ... | 0.027515 | 0.012393 | -0.000162 | 0.018565 | 0.017358 | 0.935317 | 0.127224 | 1.000000 | 0.993536 | 0.008604 |
| 243 | 0.012128 | 0.000942 | 0.044281 | 0.000235 | -0.002736 | -0.001844 | -0.000839 | -0.000888 | -0.000317 | -0.000358 | ... | 0.023072 | 0.014523 | -0.000174 | 0.021742 | 0.020331 | 0.919036 | 0.140902 | 0.993536 | 1.000000 | 0.009136 |
| 244 | 0.006612 | 0.000415 | -0.000810 | 0.000966 | 0.003656 | 0.002257 | 0.004448 | 0.002427 | -0.000739 | -0.000811 | ... | -0.003399 | -0.000773 | -0.000402 | -0.000525 | -0.000589 | 0.011106 | 0.011807 | 0.008604 | 0.009136 | 1.000000 |
227 rows × 227 columns
Let's get the list of correlated features from the data.
corrdata = corrmat.abs().stack() corrdata
0 0 1.000000
1 0.025277
2 0.001942
3 0.003594
4 0.004054
5 0.001697
6 0.015882
7 0.019807
8 0.000956
9 0.000588
10 0.012443
11 0.010319
12 0.005268
13 0.017605
14 0.016960
15 0.018040
16 0.017400
17 0.016745
18 0.015206
19 0.000103
20 0.001198
21 0.006814
22 0.002037
23 0.010356
24 0.012021
25 0.001732
26 0.001138
27 0.004836
28 0.006480
29 0.005811
...
244 215 0.000338
216 0.000244
217 0.017276
218 0.006644
219 0.018092
220 0.017579
221 0.014736
222 0.002052
223 0.014980
224 0.014628
225 0.014567
226 0.005688
227 0.015351
228 0.014485
229 0.013197
230 0.012842
231 0.013321
232 0.013418
233 0.000203
234 0.003446
235 0.003399
236 0.000773
237 0.000402
238 0.000525
239 0.000589
240 0.011106
241 0.011807
242 0.008604
243 0.009136
244 1.000000
Length: 51529, dtype: float64
Let's arrange the correlated data in the descending order.
corrdata = corrdata.sort_values(ascending=False) corrdata
29 58 1.000000e+00
58 29 1.000000e+00
134 158 1.000000e+00
158 134 1.000000e+00
182 182 1.000000e+00
181 181 1.000000e+00
159 159 1.000000e+00
160 160 1.000000e+00
161 161 1.000000e+00
162 162 1.000000e+00
163 163 1.000000e+00
164 164 1.000000e+00
165 165 1.000000e+00
166 166 1.000000e+00
167 167 1.000000e+00
168 168 1.000000e+00
169 169 1.000000e+00
170 170 1.000000e+00
171 171 1.000000e+00
158 158 1.000000e+00
173 173 1.000000e+00
174 174 1.000000e+00
175 175 1.000000e+00
176 176 1.000000e+00
177 177 1.000000e+00
183 183 1.000000e+00
178 178 1.000000e+00
179 179 1.000000e+00
180 180 1.000000e+00
172 172 1.000000e+00
...
113 60 8.925381e-06
60 113 8.925381e-06
82 193 8.892757e-06
193 82 8.892757e-06
230 110 8.848510e-06
110 230 8.848510e-06
235 15 8.707147e-06
15 235 8.707147e-06
186 243 7.715459e-06
243 186 7.715459e-06
150 120 7.232908e-06
120 150 7.232908e-06
103 189 5.738723e-06
189 103 5.738723e-06
13 120 5.200500e-06
120 13 5.200500e-06
243 162 3.905074e-06
162 243 3.905074e-06
186 126 3.594093e-06
126 186 3.594093e-06
159 242 2.877380e-06
242 159 2.877380e-06
107 68 2.392837e-06
68 107 2.392837e-06
111 229 1.934954e-06
229 111 1.934954e-06
231 150 6.044672e-07
150 231 6.044672e-07
231 123 3.966696e-07
123 231 3.966696e-07
Length: 51529, dtype: float64
Let's get the correlated data between 1 and 0.85.
corrdata = corrdata[corrdata>0.85] corrdata = corrdata[corrdata<1] corrdata
143 135 1.000000
135 143 1.000000
136 128 1.000000
128 136 1.000000
31 62 1.000000
62 31 1.000000
20 47 1.000000
47 20 1.000000
52 23 1.000000
23 52 1.000000
53 24 1.000000
24 53 1.000000
33 69 1.000000
69 33 1.000000
157 133 1.000000
133 157 1.000000
237 149 1.000000
149 237 1.000000
154 132 1.000000
132 154 1.000000
146 230 0.999997
230 146 0.999997
238 122 0.999945
122 238 0.999945
148 149 0.999929
149 148 0.999929
237 148 0.999929
148 237 0.999929
231 232 0.999892
232 231 0.999892
...
183 52 0.860163
52 183 0.860163
183 23 0.860163
23 183 0.860163
79 195 0.859806
195 79 0.859806
8 193 0.859270
193 8 0.859270
29 61 0.858830
61 29 0.858830
58 0.858830
58 61 0.858830
84 77 0.858529
77 84 0.858529
83 189 0.858484
189 83 0.858484
84 194 0.857731
194 84 0.857731
76 190 0.857717
190 76 0.857717
151 173 0.854991
173 151 0.854991
41 163 0.852233
163 41 0.852233
66 67 0.851384
67 66 0.851384
61 28 0.851022
28 61 0.851022
72 35 0.850893
35 72 0.850893
Length: 534, dtype: float64
corrdata = pd.DataFrame(corrdata).reset_index() corrdata.columns = ['features1', 'features2', 'corr_value'] corrdata
| features1 | features2 | corr_value | |
|---|---|---|---|
| 0 | 143 | 135 | 1.000000 |
| 1 | 135 | 143 | 1.000000 |
| 2 | 136 | 128 | 1.000000 |
| 3 | 128 | 136 | 1.000000 |
| 4 | 31 | 62 | 1.000000 |
| 5 | 62 | 31 | 1.000000 |
| 6 | 20 | 47 | 1.000000 |
| 7 | 47 | 20 | 1.000000 |
| 8 | 52 | 23 | 1.000000 |
| 9 | 23 | 52 | 1.000000 |
| 10 | 53 | 24 | 1.000000 |
| 11 | 24 | 53 | 1.000000 |
| 12 | 33 | 69 | 1.000000 |
| 13 | 69 | 33 | 1.000000 |
| 14 | 157 | 133 | 1.000000 |
| 15 | 133 | 157 | 1.000000 |
| 16 | 237 | 149 | 1.000000 |
| 17 | 149 | 237 | 1.000000 |
| 18 | 154 | 132 | 1.000000 |
| 19 | 132 | 154 | 1.000000 |
| 20 | 146 | 230 | 0.999997 |
| 21 | 230 | 146 | 0.999997 |
| 22 | 238 | 122 | 0.999945 |
| 23 | 122 | 238 | 0.999945 |
| 24 | 148 | 149 | 0.999929 |
| 25 | 149 | 148 | 0.999929 |
| 26 | 237 | 148 | 0.999929 |
| 27 | 148 | 237 | 0.999929 |
| 28 | 231 | 232 | 0.999892 |
| 29 | 232 | 231 | 0.999892 |
| ... | ... | ... | ... |
| 504 | 183 | 52 | 0.860163 |
| 505 | 52 | 183 | 0.860163 |
| 506 | 183 | 23 | 0.860163 |
| 507 | 23 | 183 | 0.860163 |
| 508 | 79 | 195 | 0.859806 |
| 509 | 195 | 79 | 0.859806 |
| 510 | 8 | 193 | 0.859270 |
| 511 | 193 | 8 | 0.859270 |
| 512 | 29 | 61 | 0.858830 |
| 513 | 61 | 29 | 0.858830 |
| 514 | 61 | 58 | 0.858830 |
| 515 | 58 | 61 | 0.858830 |
| 516 | 84 | 77 | 0.858529 |
| 517 | 77 | 84 | 0.858529 |
| 518 | 83 | 189 | 0.858484 |
| 519 | 189 | 83 | 0.858484 |
| 520 | 84 | 194 | 0.857731 |
| 521 | 194 | 84 | 0.857731 |
| 522 | 76 | 190 | 0.857717 |
| 523 | 190 | 76 | 0.857717 |
| 524 | 151 | 173 | 0.854991 |
| 525 | 173 | 151 | 0.854991 |
| 526 | 41 | 163 | 0.852233 |
| 527 | 163 | 41 | 0.852233 |
| 528 | 66 | 67 | 0.851384 |
| 529 | 67 | 66 | 0.851384 |
| 530 | 61 | 28 | 0.851022 |
| 531 | 28 | 61 | 0.851022 |
| 532 | 72 | 35 | 0.850893 |
| 533 | 35 | 72 | 0.850893 |
534 rows × 3 columns
Let's have a list of uncorrelated features from the dataset.
grouped_feature_list = []
correlated_groups_list = []
for feature in corrdata.features1.unique():
if feature not in grouped_feature_list:
correlated_block = corrdata[corrdata.features1 == feature]
grouped_feature_list = grouped_feature_list + list(correlated_block.features2.unique()) + [feature]
correlated_groups_list.append(correlated_block)
len(correlated_groups_list)
56
X_train.shape, X_train_uncorr.shape
((16000, 370), (16000, 103))
for group in correlated_groups_list:
print(group)
features1 features2 corr_value
0 143 135 1.0
features1 features2 corr_value
2 136 128 1.000000
197 136 169 0.959468
features1 features2 corr_value
4 31 62 1.0
features1 features2 corr_value
6 20 47 1.0
features1 features2 corr_value
8 52 23 1.000000
297 52 24 0.927683
299 52 53 0.927683
448 52 21 0.877297
505 52 183 0.860163
features1 features2 corr_value
12 33 69 1.000000
224 33 32 0.947113
228 33 68 0.946571
322 33 26 0.917665
337 33 55 0.914178
422 33 184 0.884383
features1 features2 corr_value
14 157 133 1.0
features1 features2 corr_value
16 237 149 1.000000
26 237 148 0.999929
features1 features2 corr_value
18 154 132 1.0
features1 features2 corr_value
20 146 230 0.999997
36 146 229 0.999778
59 146 231 0.997052
68 146 232 0.996772
76 146 113 0.996424
89 146 120 0.993307
245 146 170 0.944314
features1 features2 corr_value
22 238 122 0.999945
49 238 239 0.998497
264 238 236 0.938668
features1 features2 corr_value
34 82 78 0.999859
features1 features2 corr_value
40 108 115 0.999478
97 108 219 0.992870
115 108 125 0.987333
142 108 220 0.982474
280 108 217 0.933815
features1 features2 corr_value
46 199 197 0.998753
362 199 196 0.905699
371 199 198 0.904341
features1 features2 corr_value
50 181 208 0.997718
345 181 205 0.911453
467 181 207 0.871801
features1 features2 corr_value
72 17 14 0.996739
396 17 16 0.890442
408 17 13 0.888669
features1 features2 corr_value
86 242 243 0.993536
122 242 126 0.986744
276 242 240 0.935317
features1 features2 corr_value
92 28 57 0.993186
124 28 58 0.986371
126 28 29 0.986371
185 28 185 0.964067
381 28 27 0.901032
399 28 30 0.889321
531 28 61 0.851022
features1 features2 corr_value
94 51 22 0.992882
385 51 182 0.899063
features1 features2 corr_value
100 44 46 0.990593
377 44 98 0.902736
410 44 95 0.888337
features1 features2 corr_value
102 77 81 0.989793
461 77 80 0.874240
517 77 84 0.858529
features1 features2 corr_value
104 109 223 0.989341
151 109 224 0.980951
356 109 221 0.907987
413 109 111 0.887721
features1 features2 corr_value
112 9 8 0.988256
417 9 193 0.886955
444 9 192 0.878045
features1 features2 corr_value
116 227 228 0.987304
188 227 225 0.962657
features1 features2 corr_value
118 116 117 0.987013
features1 features2 corr_value
128 91 49 0.985951
features1 features2 corr_value
130 54 25 0.985875
419 54 100 0.886309
features1 features2 corr_value
134 76 75 0.984751
353 76 74 0.908497
477 76 191 0.870551
522 76 190 0.857717
features1 features2 corr_value
136 38 35 0.984077
261 38 34 0.940390
306 38 36 0.922699
496 38 72 0.864661
features1 features2 corr_value
138 18 15 0.983164
465 18 16 0.872133
470 18 13 0.870936
features1 features2 corr_value
140 215 107 0.983156
146 215 216 0.981815
features1 features2 corr_value
161 56 61 0.976942
187 56 27 0.962726
211 56 30 0.953194
features1 features2 corr_value
164 162 163 0.975002
288 162 161 0.930635
369 162 164 0.904702
463 162 41 0.874083
features1 features2 corr_value
166 102 103 0.974341
features1 features2 corr_value
168 83 79 0.973140
263 83 188 0.938960
273 83 84 0.936080
315 83 194 0.919405
351 83 80 0.910385
518 83 189 0.858484
features1 features2 corr_value
174 70 72 0.972088
500 70 35 0.862850
features1 features2 corr_value
180 59 60 0.968504
features1 features2 corr_value
207 195 189 0.956666
313 195 80 0.920961
330 195 194 0.916442
378 195 84 0.902276
428 195 188 0.882312
509 195 79 0.859806
features1 features2 corr_value
216 235 234 0.950232
349 235 106 0.911179
features1 features2 corr_value
220 10 104 0.948845
features1 features2 corr_value
234 180 179 0.945288
features1 features2 corr_value
236 241 151 0.944812
features1 features2 corr_value
243 42 41 0.944451
415 42 161 0.887059
503 42 164 0.861507
features1 features2 corr_value
248 12 5 0.943622
434 12 11 0.881673
features1 features2 corr_value
266 4 11 0.938409
402 4 5 0.888789
features1 features2 corr_value
274 93 92 0.935867
features1 features2 corr_value
290 89 121 0.928898
features1 features2 corr_value
304 88 87 0.924
features1 features2 corr_value
318 174 204 0.918533
features1 features2 corr_value
333 50 21 0.916137
features1 features2 corr_value
354 6 7 0.908158
features1 features2 corr_value
372 64 65 0.904095
488 64 87 0.866430
features1 features2 corr_value
374 101 86 0.903641
394 101 40 0.892951
features1 features2 corr_value
390 131 153 0.89633
features1 features2 corr_value
525 173 151 0.854991
features1 features2 corr_value
528 66 67 0.851384
Feature Importance based on tree based classifiers
Let's get the list of important features from the following code.
important_features = []
for group in correlated_groups_list:
features = list(group.features1.unique()) + list(group.features2.unique())
rf = RandomForestClassifier(n_estimators=100, random_state=0)
rf.fit(X_train_unique[features], y_train)
importance = pd.concat([pd.Series(features), pd.Series(rf.feature_importances_)], axis = 1)
importance.columns = ['features', 'importance']
importance.sort_values(by = 'importance', ascending = False, inplace = True)
feat = importance.iloc[0]
important_features.append(feat)
important_features
[features 135.00 importance 0.51 Name: 1, dtype: float64, features 128.000000 importance 0.563757 Name: 1, dtype: float64, features 62.00 importance 0.51 Name: 1, dtype: float64, features 47.00 importance 0.51 Name: 1, dtype: float64, features 183.000000 importance 0.285817 Name: 5, dtype: float64, features 184.00000 importance 0.34728 Name: 6, dtype: float64, features 157.00 importance 0.34 Name: 0, dtype: float64, features 148.000000 importance 0.505844 Name: 2, dtype: float64, features 132.00 importance 0.39 Name: 1, dtype: float64, features 120.000000 importance 0.749683 Name: 6, dtype: float64, features 122.00 importance 0.34 Name: 1, dtype: float64, features 82.000000 importance 0.518827 Name: 0, dtype: float64, features 125.000000 importance 0.940524 Name: 3, dtype: float64, features 197.000000 importance 0.289727 Name: 1, dtype: float64, features 207.000000 importance 0.312834 Name: 3, dtype: float64, features 17.000000 importance 0.286833 Name: 0, dtype: float64, features 243.000000 importance 0.431557 Name: 1, dtype: float64, features 185.000000 importance 0.391367 Name: 4, dtype: float64, features 182.000000 importance 0.432045 Name: 2, dtype: float64, features 95.000000 importance 0.487162 Name: 3, dtype: float64, features 84.000000 importance 0.299008 Name: 3, dtype: float64, features 221.00000 importance 0.28555 Name: 3, dtype: float64, features 8.000000 importance 0.345509 Name: 1, dtype: float64, features 228.000000 importance 0.434186 Name: 1, dtype: float64, features 117.000000 importance 0.517013 Name: 1, dtype: float64, features 49.000000 importance 0.500161 Name: 1, dtype: float64, features 100.000000 importance 0.386775 Name: 2, dtype: float64, features 191.000000 importance 0.345104 Name: 3, dtype: float64, features 34.000000 importance 0.283901 Name: 2, dtype: float64, features 15.000000 importance 0.400677 Name: 1, dtype: float64, features 107.000000 importance 0.349126 Name: 1, dtype: float64, features 61.000000 importance 0.323735 Name: 1, dtype: float64, features 41.000000 importance 0.386338 Name: 4, dtype: float64, features 102.000000 importance 0.508955 Name: 0, dtype: float64, features 189.000000 importance 0.229269 Name: 6, dtype: float64, features 72.000000 importance 0.490102 Name: 1, dtype: float64, features 60.00000 importance 0.50052 Name: 1, dtype: float64, features 79.000000 importance 0.213903 Name: 6, dtype: float64, features 234.000000 importance 0.445719 Name: 1, dtype: float64, features 104.000000 importance 0.640915 Name: 1, dtype: float64, features 179.000000 importance 0.634779 Name: 1, dtype: float64, features 151.00 importance 0.51 Name: 1, dtype: float64, features 161.000000 importance 0.346426 Name: 2, dtype: float64, features 5.000000 importance 0.356386 Name: 1, dtype: float64, features 5.000000 importance 0.403831 Name: 2, dtype: float64, features 93.000000 importance 0.544349 Name: 0, dtype: float64, features 121.00 importance 0.51 Name: 1, dtype: float64, features 87.000000 importance 0.553622 Name: 1, dtype: float64, features 174.000000 importance 0.743723 Name: 0, dtype: float64, features 50.000000 importance 0.616659 Name: 0, dtype: float64, features 7.000000 importance 0.545702 Name: 1, dtype: float64, features 87.0000 importance 0.7462 Name: 2, dtype: float64, features 86.000000 importance 0.447693 Name: 1, dtype: float64, features 153.00 importance 0.51 Name: 1, dtype: float64, features 151.00 importance 0.51 Name: 1, dtype: float64, features 66.000000 importance 0.630293 Name: 0, dtype: float64]
important_features = pd.DataFrame(important_features) important_features.reset_index(inplace=True, drop = True)
important_features
| features | importance | |
|---|---|---|
| 0 | 135.0 | 0.510000 |
| 1 | 128.0 | 0.563757 |
| 2 | 62.0 | 0.510000 |
| 3 | 47.0 | 0.510000 |
| 4 | 183.0 | 0.285817 |
| 5 | 184.0 | 0.347280 |
| 6 | 157.0 | 0.340000 |
| 7 | 148.0 | 0.505844 |
| 8 | 132.0 | 0.390000 |
| 9 | 120.0 | 0.749683 |
| 10 | 122.0 | 0.340000 |
| 11 | 82.0 | 0.518827 |
| 12 | 125.0 | 0.940524 |
| 13 | 197.0 | 0.289727 |
| 14 | 207.0 | 0.312834 |
| 15 | 17.0 | 0.286833 |
| 16 | 243.0 | 0.431557 |
| 17 | 185.0 | 0.391367 |
| 18 | 182.0 | 0.432045 |
| 19 | 95.0 | 0.487162 |
| 20 | 84.0 | 0.299008 |
| 21 | 221.0 | 0.285550 |
| 22 | 8.0 | 0.345509 |
| 23 | 228.0 | 0.434186 |
| 24 | 117.0 | 0.517013 |
| 25 | 49.0 | 0.500161 |
| 26 | 100.0 | 0.386775 |
| 27 | 191.0 | 0.345104 |
| 28 | 34.0 | 0.283901 |
| 29 | 15.0 | 0.400677 |
| 30 | 107.0 | 0.349126 |
| 31 | 61.0 | 0.323735 |
| 32 | 41.0 | 0.386338 |
| 33 | 102.0 | 0.508955 |
| 34 | 189.0 | 0.229269 |
| 35 | 72.0 | 0.490102 |
| 36 | 60.0 | 0.500520 |
| 37 | 79.0 | 0.213903 |
| 38 | 234.0 | 0.445719 |
| 39 | 104.0 | 0.640915 |
| 40 | 179.0 | 0.634779 |
| 41 | 151.0 | 0.510000 |
| 42 | 161.0 | 0.346426 |
| 43 | 5.0 | 0.356386 |
| 44 | 5.0 | 0.403831 |
| 45 | 93.0 | 0.544349 |
| 46 | 121.0 | 0.510000 |
| 47 | 87.0 | 0.553622 |
| 48 | 174.0 | 0.743723 |
| 49 | 50.0 | 0.616659 |
| 50 | 7.0 | 0.545702 |
| 51 | 87.0 | 0.746200 |
| 52 | 86.0 | 0.447693 |
| 53 | 153.0 | 0.510000 |
| 54 | 151.0 | 0.510000 |
| 55 | 66.0 | 0.630293 |
Let's get the features which are to be discarded.
features_to_consider = set(important_features['features']) features_to_discard = set(corr_features) - set(features_to_consider) features_to_discard = list(features_to_discard) X_train_grouped_uncorr = X_train_unique.drop(labels = features_to_discard, axis = 1)
Let's get the shape of the uncorrelated dataset.
X_train_grouped_uncorr.shape
(16000, 140)
X_test_grouped_uncorr = X_test_unique.drop(labels=features_to_discard, axis = 1) X_test_grouped_uncorr.shape
(4000, 140)
%%time run_randomForest(X_train_grouped_uncorr, X_test_grouped_uncorr, y_train, y_test)
Accuracy on test set: 0.95775 Wall time: 1.01 s
%%time run_randomForest(X_train, X_test, y_train, y_test)
Accuracy on test set: 0.9585 Wall time: 1.48 s
%%time run_randomForest(X_train_uncorr, X_test_uncorr, y_train, y_test)
Accuracy on test set: 0.95875 Wall time: 891 ms
3 Comments