What is K-Mean Clustering?

Machine Learning can broadly be classified into three types:

1. Supervised Learning
2. Unsupervised Learning
3. Semi-supervised Learning

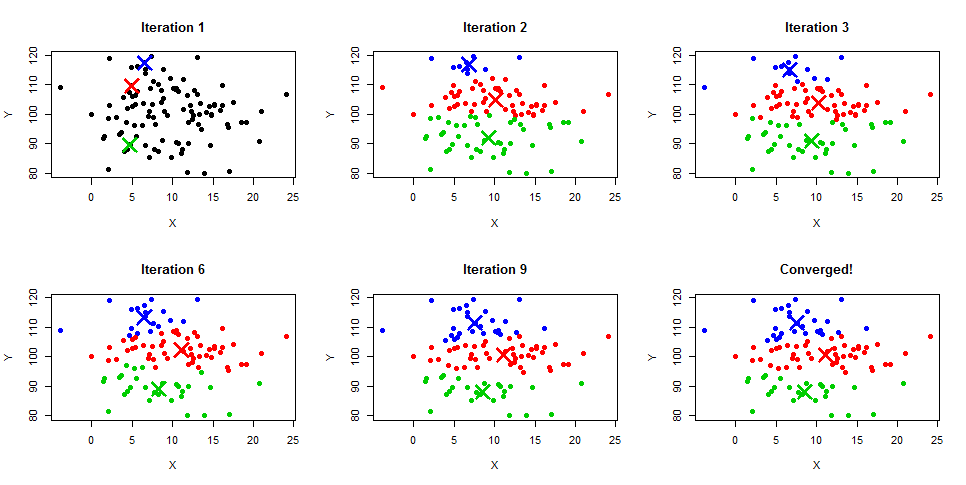
K-means algorithm identifies k number of centroids, and then allocates every data point to the nearest cluster, while keeping the centroids as small as possible. The ‘means’ in the K-means refers to averaging of the data; that is, finding the centroid.

Types of clustering

• Hard clustering
• Soft clustering

Type of Clustering Algorithms

Connectivity-based clustering

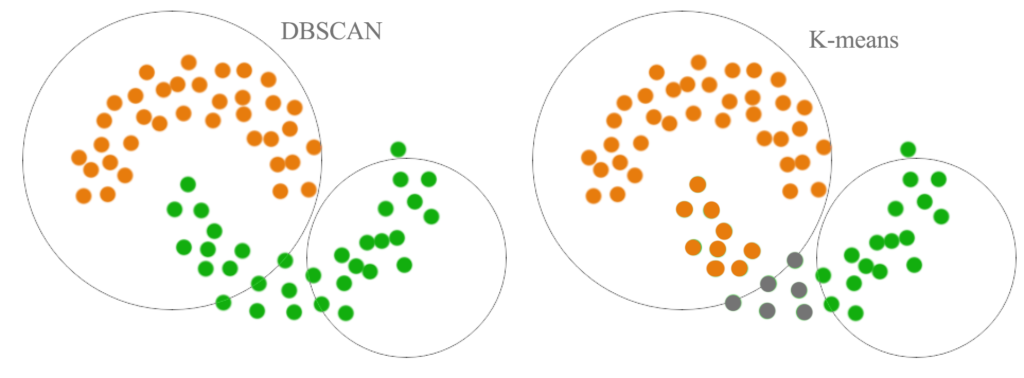
The main idea behind this clustering is that data points that are closer in the data space are more related (similar) than to data points farther away. They are also not very robust towards outliers, which might show up as additional clusters or even cause other clusters to merge.

Centroid-based clustering

In this type of clustering, clusters are represented by a central vector or a centroid. This centroid might not necessarily be a member of the dataset.

Distribution-based clustering

These models have a strong theoritical foundation, however they often suffer from overfitting. Gaussian mixture models, using the expectation-maximization algorithm is a famous distribution based clustering method.

Density-based methods search the data space for areas of varied density of data points.

Dataset and Problem Understanding

At first we will be importing certain libraries which we will need to work on the given dataset.

Pandas which offers data structures and operation for manipulating numerical tables.

Seaborn and matplotlib for data visualizations.

Also numpy for working on array.

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline

Fetching the data using pandas.

data = pd.read_csv('data.csv', index_col = 0)
data.head()

	x	y	cluster
0	-8.482852	-5.603349	2
1	-7.751632	-8.405334	2
2	-10.967098	-9.032782	2
3	-11.999447	-7.606734	2
4	-1.736810	10.478015	1

Let's look at the top five rows using the Dataframe's head() method. you can find out what all categories exist and how many instances(row) belong to each category by using value_counts() method .

data['cluster'].value_counts()

1    67
0    67
2    66
Name: cluster, dtype: int64

So, we have 67 dataset each which belong to cluster 1 and cluster 0 and 66 dataset belong to cluster 2.

Now we can a scatter plot of the dataset and visualize the cluster formed.

We have matplotlib library which we have already impoted above to plot the dataset. So before you can plot anything, you need to specify which backend Matplotlib should use. The simplest option is to use Jupyter’s magic command %matplotlib inline. This tells Jupyter to set up Matplotlib so it uses Jupyter’s own backend.

plt.scatter(data['x'], data['y'], c = data['cluster'], cmap = 'viridis')
plt.xlabel('X-values')
plt.ylabel('Y-values')
plt.title('Formation of cluster')
plt.show()

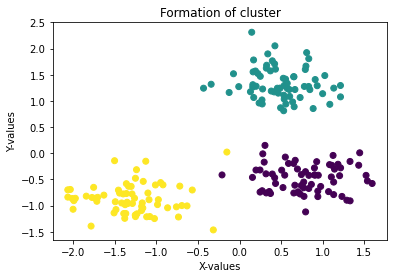
K-Means for clustering

The K-Means algorithm is a simple algorithm capable of clustering the same kind of dataset very quickly and efficiently, often in just a few iterations.Its an unsupervised machine learning technique.

Let's train a K-Means cluster on this dataset. It will try to find each blob's center and assign each instance to the closed blob.

Importing K - Means from sklearn cluster at first.

from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler

X = data[['x', 'y']]
y = data['cluster']

We standardize the dataset before training the algorithm because the variable can of incomparable units (eg one in cm other in kg) so we should standardize variables, ofcourse. Also when the data show quite a different variances it is a good practice to standardize the data

scaler = StandardScaler()
X = scaler.fit_transform(X)
X[: 5]

array([[-1.01200363, -0.60606415],
       [-0.86550679, -1.04265203],
       [-1.5097118 , -1.14041707],
       [-1.71653856, -0.91821912],
       [ 0.33953731,  1.89963378]])

Now we impute back the standardized data in our dataset and train the algorithm.

data[['x', 'y']] = X

We are taking the number of clusters k as two for time being.

Note that you have to specify the number of clusters k that the algorithm must find. In this dataset, it is pretty obvious from looking at the data that k should be set to 3, but we choose it 2 as of now. Also in general it is not that easy to find the number of clusters.

Later we will see the method to find the optimal number of cluster for a dataset.

k=2
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(X)

KMeans(n_clusters=2, random_state=42)

We will take a look at the two centroid that the algorithm found:

center = kmeans.cluster_centers_
center

array([[-1.30618271, -0.87560626],
       [ 0.64334372,  0.43126875]])

Now plotting the dataset and each centroid.

plt.scatter(data['x'], data['y'], c = kmeans.labels_, cmap = 'viridis')
plt.xlabel('X-values')
plt.ylabel('Y-values')
plt.title('Formation of cluster with centroids')
for i, point in enumerate(center):
    plt.plot(center[i][0], center[i][1], '*r--', linewidth=2, markersize=18)

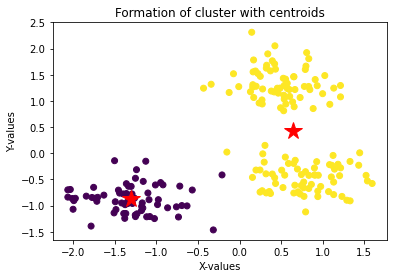
With number of cluster as 2 thecentroid (marked as red star above) are pretty obivious.

plt.scatter(data['x'], data['y'], c = data['cluster'], cmap = 'viridis')
plt.xlabel('X-values')
plt.ylabel('Y-values')
plt.title('Formation of 3-cluster')
plt.show()

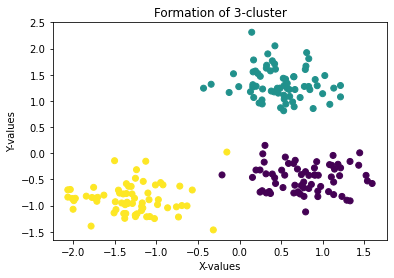
here we can easily visualize 3 clusters. So, now we will see how we can find out the right value for K (number of cluster)

How do I choose right value of k?

you need to understand how it works?

Assuming we have inputs x_1, x_2, x_3, ..., x_nx

• Step 1 - Pick K random points as cluster centers called centroids.
• Step 2 - Assign each x_i to nearest cluster by calculating its distance to each centroid.
• Step 3 - Find new cluster center by taking the average of the assigned points.
• Step 4 - Repeat Step 2 and 3 until none of the cluster assignments change.

Most important, when to stop increasing K?

We often know the value of K. In that case we use the value of K. Else we use the Elbow Method.

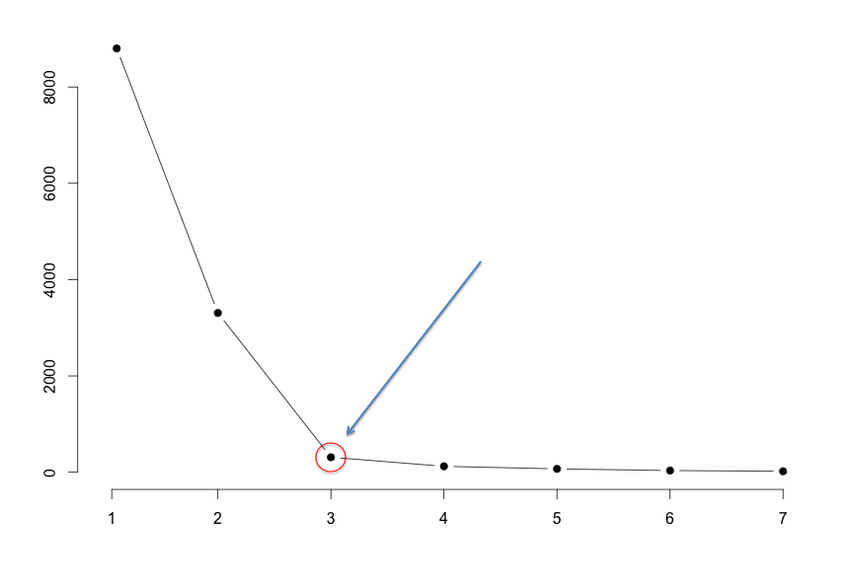
Error Sum of Squares (SSE)

It is the sum of the squared differences between each observation and its group's mean. We can use it as a measure of variation within a cluster. All cases within a cluster are identical then SSE would be equal to 0. We run the algorithm for different values of K(say K = 10 to 1) and plot the K values against SSE(Sum of Squared Errors). And select the value of K for the elbow point as shown in the figure.

$$ \text SSE = \sum_{i=1}^k\left(\sum_{x_j \subset S_i}||x_j-\mu_i||^2\right) $$

So we try value for k between 1 to 10 and use elbow method as explaind above.

SSE = []
index = range(1,10)
for i in index:
    kmeans = KMeans(n_clusters=i, random_state=42)
    kmeans.fit(X)
    SSE.append(kmeans.inertia_)
    print(kmeans.inertia_)

400.0000000000001
156.41078579574975
44.057048453292815
36.726387118666075
31.01642761531463
25.39959047192452
22.547184727743304
19.92343817847746
17.295836404824982

Here the metric inertia is nothing but the mean squared distance between each instance and its closest centroid.

plt.plot(index, SSE)
plt.xlabel('K')
plt.ylabel('SEE')
plt.title('SSE with respect to K')
plt.show()

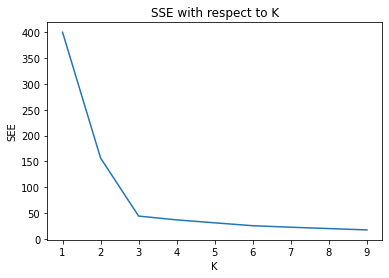
From the graph, we can observe with increasing the K value SSE will decrease. So, like mentioned before the value of k should be 3. Now lets do it again with k=3

k=3
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(X)
KMeans(n_clusters=3, random_state=42)
center = kmeans.cluster_centers_
plt.xlabel('X-values')
plt.ylabel('Y-values')
plt.title('Formation of clusters with 3-centroids')

plt.scatter(data['x'], data['y'], c = kmeans.labels_, cmap = 'viridis')
for i, point in enumerate(center):
plt.plot(center[i][0], center[i][1], '*r--', linewidth=2, markersize=18)

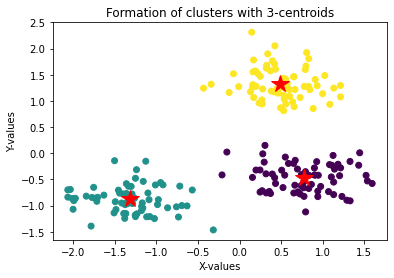
Let's go ahead and explore it in a little bit more detail

Use Iris dataset

from sklearn import datasets

iris = datasets.load_iris()
X = iris.data
scaler = StandardScaler()
X = scaler.fit_transform(X)
iris.target_names

array(['setosa', 'versicolor', 'virginica'], dtype='<U10')

SSE = []
index = range(1,10)
for i in index:
    kmeans = KMeans(n_clusters=i, random_state=42)
    kmeans.fit(X)
    SSE.append(kmeans.inertia_)
    print(kmeans.inertia_)

600.0
222.36170496502302
139.82049635974974
114.41256181896094
90.92751382392049
80.0224959955744
71.81624598106144
62.28749580350205
54.8110520315013

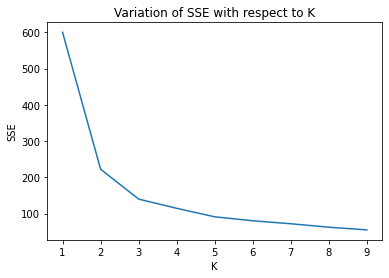
plt.plot(index, SSE)
plt.xlabel('K')
plt.ylabel('SSE')
plt.title('Variation of SSE with respect to K')
plt.show()