Feature Selection Based on Univariate (ANOVA) Test for Classification | Machine Learning | KGP Talkie
Feature Selection Based on Univariate (ANOVA) Test for Classification
Watch Full Playlist: https://www.youtube.com/playlist?list=PLc2rvfiptPSQYzmDIFuq2PqN2n28ZjxDH
What is Univariate (ANOVA) Test
The elimination process aims to reduce the size of the input feature set and at the same time to retain the class discriminatory information for classification problems.

An F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis.
Analysis of variance (ANOVA) is a collection of statistical models and their associated estimation procedures (such as the “variation” among and between groups) used to analyze the differences among group means in a sample.
The F-test is used for comparing the factors of the total deviation. For example, in one-way, or single-factor ANOVA, statistical significance is tested for by comparing the F test statistic
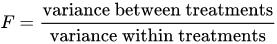
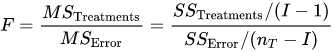

Classification Problem
Importing required libraries
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns
from sklearn.model_selection import train_test_split from sklearn.ensemble import RandomForestClassifier from sklearn.metrics import accuracy_score from sklearn.feature_selection import VarianceThreshold from sklearn.feature_selection import f_classif, f_regression from sklearn.feature_selection import SelectKBest, SelectPercentile
Download DataFiles: https://github.com/laxmimerit/Data-Files-for-Feature-Selection
data = pd.read_csv('train.csv', nrows = 20000)
data.head()| ID | var3 | var15 | imp_ent_var16_ult1 | imp_op_var39_comer_ult1 | imp_op_var39_comer_ult3 | imp_op_var40_comer_ult1 | imp_op_var40_comer_ult3 | imp_op_var40_efect_ult1 | imp_op_var40_efect_ult3 | … | saldo_medio_var33_hace2 | saldo_medio_var33_hace3 | saldo_medio_var33_ult1 | saldo_medio_var33_ult3 | saldo_medio_var44_hace2 | saldo_medio_var44_hace3 | saldo_medio_var44_ult1 | saldo_medio_var44_ult3 | var38 | TARGET | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 23 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0 | 0 | … | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 39205.170000 | 0 |
| 1 | 3 | 2 | 34 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0 | 0 | … | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 49278.030000 | 0 |
| 2 | 4 | 2 | 23 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0 | 0 | … | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 67333.770000 | 0 |
| 3 | 8 | 2 | 37 | 0.0 | 195.0 | 195.0 | 0.0 | 0.0 | 0 | 0 | … | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 64007.970000 | 0 |
| 4 | 10 | 2 | 39 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0 | 0 | … | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 117310.979016 | 0 |
5 rows × 371 columns
X = data.drop('TARGET', axis = 1)
y = data['TARGET']
X.shape, y.shape
((20000, 370), (20000,))
Now train, test and split the data with test size equals to 0.2.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0, stratify = y)
Remove Constant, Quasi Constant, and Correlated Features
These are the filters that are almost constant or quasi constant in other words these features have same values for large subset of outputs and such features are not very useful for making predictions
Let’s remove the constant and quasi constant features with the following code.
constant_filter = VarianceThreshold(threshold=0.01) constant_filter.fit(X_train) X_train_filter = constant_filter.transform(X_train) X_test_filter = constant_filter.transform(X_test)
Let’s get the shape of the filtered data.
X_train_filter.shape, X_test_filter.shape
((16000, 245), (4000, 245))
If two features are exactly same those are called as duplicate features that means these features doesn’t provide any new information and makes our model complex.
Here we have a problem as we did in quasi constant and constant removal sklearn doesn’t have direct library to handle with duplicate features .
So, first we will do transpose the dataset and then python have a method to remove duplicate features.
Let’s remove the duplicated features by using the following code.
X_train_T = X_train_filter.T X_test_T = X_test_filter.T
X_train_T = pd.DataFrame(X_train_T) X_test_T = pd.DataFrame(X_test_T)
Let’s get the total number of duplicated features.
X_train_T.duplicated().sum()
18
duplicated_features = X_train_T.duplicated()
Now, we will find out the non duplicated features from the dataset.
features_to_keep = [not index for index in duplicated_features] X_train_unique = X_train_T[features_to_keep].T X_test_unique = X_test_T[features_to_keep].T
X_train_unique.shape, X_train.shape
((16000, 227), (16000, 370))
Now do F-Test
sel = f_classif(X_train_unique, y_train) sel
(array([3.42911520e-01, 1.22929093e+00, 1.61291330e+02, 4.01025132e-01,
8.37661151e-01, 2.39279390e-03, 4.41633351e-02, 1.36337510e-01,
1.84647123e+00, 2.03640367e+00, 7.98057954e-03, 1.14063993e+00,
6.32266614e-03, 1.55626237e+01, 1.53553790e+01, 1.28615978e+01,
1.61834746e+01, 1.59638013e+01, 1.21977511e+01, 9.03776687e-02,
1.00443179e+00, 1.53946148e+01, 2.50428951e+02, 2.98696944e+01,
1.06266841e+01, 2.63630437e+01, 1.66417611e+01, 3.13699473e+01,
2.47256550e+01, 2.60021376e+01, 3.26742018e+01, 9.94259060e+00,
1.48208220e+01, 1.50040146e+01, 1.34739830e+01, 7.03118653e+00,
1.36234772e+01, 7.95962134e+00, 3.15161070e+02, 1.79631284e+00,
1.66910747e+00, 1.21138302e+01, 1.10928892e+01, 1.00443179e+00,
2.31851572e+00, 8.93973153e+01, 7.53868668e+00, 2.38490562e+02,
2.98696944e+01, 1.06266841e+01, 2.61694409e+01, 1.66053267e+01,
2.93013259e+01, 2.44433356e+01, 2.60021376e+01, 5.59623841e+00,
5.65080530e+00, 3.11715028e+01, 9.94259060e+00, 6.69237272e-01,
6.73931889e-01, 5.91355150e-01, 2.16653744e+00, 1.57036464e+00,
1.48180592e+01, 1.50040146e+01, 4.10147572e+00, 5.08119829e+00,
2.86061739e-01, 4.74076524e-04, 3.22895933e-02, 3.61497992e+00,
2.62641383e-01, 1.44465136e+00, 2.39577575e+00, 3.25151692e+00,
2.66120176e-01, 1.33584657e+00, 2.15986976e+00, 2.95680783e+01,
2.74320562e+02, 1.79136749e+00, 1.65942415e+00, 4.55732338e-01,
8.03423196e+01, 5.33753163e+00, 3.43569515e+00, 5.38991827e+00,
6.48705021e+00, 1.14907051e+01, 2.46676043e+02, 1.48964854e+00,
1.48528608e+00, 1.35499717e+00, 5.04105291e+00, 8.00857735e-02,
5.92081628e-01, 7.49538059e+00, 1.43768803e+01, 3.96797511e+00,
1.84630418e+01, 5.93034025e-01, 6.23117305e-02, 1.32846978e-01,
7.36058444e+00, 4.67453255e-01, 6.53434886e-01, 2.32603599e+01,
8.82160365e-02, 4.03681937e-01, 1.12281656e-01, 1.22229167e+00,
9.50849020e+00, 3.31504999e-01, 1.52799424e+02, 9.58201843e-01,
3.81283407e-01, 8.05456673e-01, 2.11768899e-01, 4.23427422e-02,
4.23427422e-02, 4.23427422e-02, 4.23675848e-01, 9.58201843e-01,
8.05456673e-01, 4.23675848e-01, 7.83475034e+00, 7.84514734e-01,
4.28901812e-02, 1.44260945e-01, 4.33508271e-02, 4.23427422e-02,
3.34880062e-02, 1.90957786e-01, 4.06328805e-01, 1.70136127e-01,
4.23427422e-02, 5.36587189e-01, 1.87563339e+00, 4.23427422e-02,
4.23427422e-02, 4.23427422e-02, 1.25864897e-01, 1.50227029e-01,
7.58252261e-01, 3.69870284e-01, 6.31366809e-02, 1.39484806e+00,
5.24649450e+00, 8.74444426e-02, 1.20564528e+01, 1.08123286e+00,
8.46910021e-02, 2.36606015e-01, 5.89389684e+00, 2.77252663e-01,
4.15074036e-01, 1.44558159e-01, 1.17723957e+00, 9.22407334e-01,
1.45895164e+01, 1.86656969e+00, 5.43234215e+00, 1.86971763e-02,
3.09123385e+02, 7.12088878e+00, 1.49660894e+01, 2.43275497e+01,
4.52466899e+00, 2.03980835e-01, 5.87673213e-03, 4.98543138e-02,
5.16359722e-02, 1.09646850e-01, 2.06155459e+00, 2.99184059e+00,
2.21995621e-02, 1.13858713e-01, 1.14255501e+01, 1.13785982e+01,
1.19082872e+01, 1.18528440e+01, 2.65465286e-02, 1.52894509e-01,
4.63685902e+00, 2.10080736e+00, 1.65523608e-01, 2.16891078e-01,
1.40302586e+00, 5.48359285e-01, 6.35218588e-02, 4.88987865e+00,
2.49656443e+00, 4.58216058e+00, 4.15099427e+00, 4.56305342e-01,
1.66491238e-01, 3.90777488e-01, 3.50953637e-01, 5.52484208e+00,
2.37194124e+00, 7.35792170e+00, 7.47930913e+00, 1.19139338e+01,
3.63667170e+00, 1.46817492e+01, 1.40921857e+01, 2.55113543e+00,
7.93363123e-01, 2.95584767e+00, 2.83339311e+00, 4.73780486e-02,
4.26696894e-02, 6.24420202e-02, 6.13788649e-02, 5.70774760e-02,
7.65160310e-02, 1.10327676e-01, 1.26598304e-01, 4.23427422e-02,
1.11726086e-01, 1.17106404e-01, 3.13117156e-01, 1.24267517e-01,
2.84184735e-01, 3.29540269e-01, 1.12297080e+01]),
array([5.58161700e-01, 2.67561647e-01, 8.89333290e-37, 5.26569363e-01,
3.60080335e-01, 9.60986695e-01, 8.33552698e-01, 7.11954403e-01,
1.74213527e-01, 1.53591870e-01, 9.28817521e-01, 2.85533263e-01,
9.36623841e-01, 8.01575252e-05, 8.94375507e-05, 3.36393721e-04,
5.77577141e-05, 6.48544590e-05, 4.79763179e-04, 7.63701483e-01,
3.16255673e-01, 8.76012543e-05, 5.56578484e-56, 4.68990120e-08,
1.11700314e-03, 2.86219940e-07, 4.53647534e-05, 2.16766394e-08,
6.67830586e-07, 3.44933857e-07, 1.10916535e-08, 1.61796584e-03,
1.18682969e-04, 1.07709938e-04, 2.42680916e-04, 8.01812206e-03,
2.24116226e-04, 4.78913410e-03, 7.66573763e-70, 1.80177928e-01,
1.96396787e-01, 5.01825968e-04, 8.68554202e-04, 3.16255673e-01,
1.27861727e-01, 3.66783202e-21, 6.04554908e-03, 2.03825983e-53,
4.68990120e-08, 1.11700314e-03, 3.16348432e-07, 4.62436764e-05,
6.28457802e-08, 7.73029885e-07, 3.44933857e-07, 1.80109375e-02,
1.74590458e-02, 2.40048097e-08, 1.61796584e-03, 4.13329839e-01,
4.11696353e-01, 4.41906921e-01, 1.41063166e-01, 2.10172382e-01,
1.18856798e-04, 1.07709938e-04, 4.28623726e-02, 2.42001211e-02,
5.92762818e-01, 9.82629065e-01, 8.57395823e-01, 5.72793629e-02,
6.08318344e-01, 2.29405921e-01, 1.21683164e-01, 7.13761984e-02,
6.05953475e-01, 2.47785024e-01, 1.41676361e-01, 5.47783585e-08,
4.18717532e-61, 1.80778657e-01, 1.97699723e-01, 4.99635011e-01,
3.49020462e-19, 2.08836652e-02, 6.38201266e-02, 2.02659144e-02,
1.08755946e-02, 7.01140336e-04, 3.55791184e-55, 2.22288988e-01,
2.22967265e-01, 2.44423761e-01, 2.47670413e-02, 7.77184868e-01,
4.41626654e-01, 6.19258331e-03, 1.50177954e-04, 4.63904749e-02,
1.74254389e-05, 4.41259644e-01, 8.02881978e-01, 7.15503084e-01,
6.67404495e-03, 4.94171032e-01, 4.18899308e-01, 1.42788438e-06,
7.66461321e-01, 5.25202939e-01, 7.37565700e-01, 2.68928005e-01,
2.04871607e-03, 5.64782330e-01, 6.11812415e-35, 3.27655140e-01,
5.36925966e-01, 3.69480411e-01, 6.45390733e-01, 8.36970444e-01,
8.36970444e-01, 8.36970444e-01, 5.15117892e-01, 3.27655140e-01,
3.69480411e-01, 5.15117892e-01, 5.13125866e-03, 3.75777233e-01,
8.35934829e-01, 7.04086312e-01, 8.35068733e-01, 8.36970444e-01,
8.54802468e-01, 6.62126552e-01, 5.23847887e-01, 6.79996382e-01,
8.36970444e-01, 4.63861289e-01, 1.70850496e-01, 8.36970444e-01,
8.36970444e-01, 8.36970444e-01, 7.22763262e-01, 6.98323652e-01,
3.83889093e-01, 5.43083617e-01, 8.01608490e-01, 2.37605638e-01,
2.20039777e-02, 7.67455348e-01, 5.17497373e-04, 2.98437634e-01,
7.71041949e-01, 6.26674911e-01, 1.52044006e-02, 5.98514898e-01,
5.19414532e-01, 7.03796034e-01, 2.77935032e-01, 3.36858193e-01,
1.34160887e-04, 1.71887678e-01, 1.97795129e-02, 8.91239914e-01,
1.49493801e-68, 7.62677506e-03, 1.09894509e-04, 8.20840983e-07,
3.34247932e-02, 6.51532760e-01, 9.38895107e-01, 8.23319823e-01,
8.20243529e-01, 7.40550887e-01, 1.51075546e-01, 8.37042875e-02,
8.81559318e-01, 7.35797526e-01, 7.26140977e-04, 7.44713683e-04,
5.60290090e-04, 5.77206713e-04, 8.70574777e-01, 6.95789674e-01,
3.13071224e-02, 1.47240985e-01, 6.84126595e-01, 6.41425380e-01,
2.36235196e-01, 4.58999733e-01, 8.01016915e-01, 2.70286705e-02,
1.14114721e-01, 3.23215275e-02, 4.16265059e-02, 4.99365521e-01,
6.83254631e-01, 5.31899920e-01, 5.53582168e-01, 1.87603701e-02,
1.23553129e-01, 6.68393143e-03, 6.24807382e-03, 5.58595551e-04,
5.65377099e-02, 1.27759206e-04, 1.74681308e-04, 1.10234773e-01,
3.73098519e-01, 8.55867690e-02, 9.23426211e-02, 8.27692918e-01,
8.36351110e-01, 8.02680255e-01, 8.04332893e-01, 8.11179263e-01,
7.82079079e-01, 7.39775741e-01, 7.21990132e-01, 8.36970444e-01,
7.38191886e-01, 7.32198763e-01, 5.75781477e-01, 7.24455979e-01,
5.93978825e-01, 5.65937990e-01, 8.06846135e-04]))Let’s arrange the values in ascending order.
p_values = pd.Series(sel[1]) p_values.index = X_train_unique.columns p_values.sort_values(ascending = True, inplace = True)
Let’s plot the pvalues with respect to the features using the bar plot.
p_values.plot.bar(figsize = (16, 5))
plt.title('pvalues with respect to features')
plt.show()
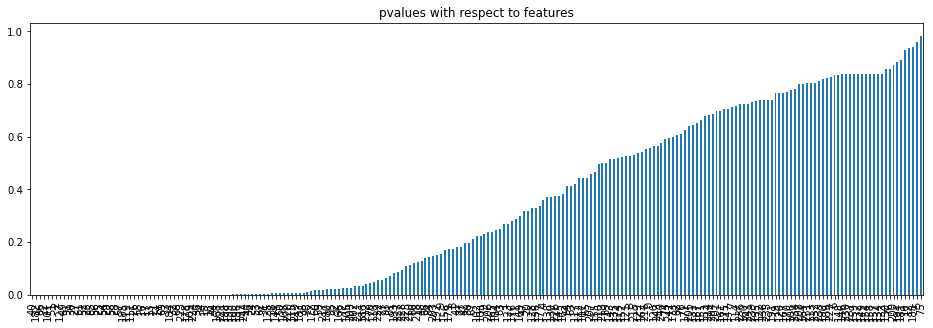
p_values = p_values[p_values<0.05]
p_values.index
Int64Index([ 40, 182, 86, 22, 101, 51, 2, 127, 49, 91, 30, 27, 61,
52, 23, 85, 56, 25, 54, 29, 58, 28, 57, 185, 119, 111,
26, 55, 16, 17, 13, 21, 14, 69, 33, 184, 32, 68, 223,
178, 109, 224, 36, 34, 15, 18, 44, 168, 221, 198, 199, 100,
196, 197, 244, 46, 24, 53, 62, 31, 125, 38, 144, 50, 108,
220, 115, 219, 183, 35, 98, 172, 60, 59, 217, 180, 95, 92,
166, 72, 105, 209, 202, 211, 186, 212, 70, 110],
dtype='int64')X_train_p = X_train_unique[p_values.index] X_test_p = X_test_unique[p_values.index]
Build the classifiers and compare the performance
Let’s build the Random forest classifier and then get the predicted y value.
def run_randomForest(X_train, X_test, y_train, y_test):
clf = RandomForestClassifier(n_estimators=100, random_state=0, n_jobs = -1)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('Accuracy: ', accuracy_score(y_test, y_pred))
Let’s calculate the accuracy and training time of trained dataset.
%%time run_randomForest(X_train_p, X_test_p, y_train, y_test)
Accuracy: 0.953 Wall time: 814 ms
Let’s calculate the accuracy and training time of original dataset.
%%time run_randomForest(X_train, X_test, y_train, y_test)
Accuracy: 0.9585 Wall time: 1.49 s

0 Comments